Calculating States Using Diagrams
Rules for Hamiltonians
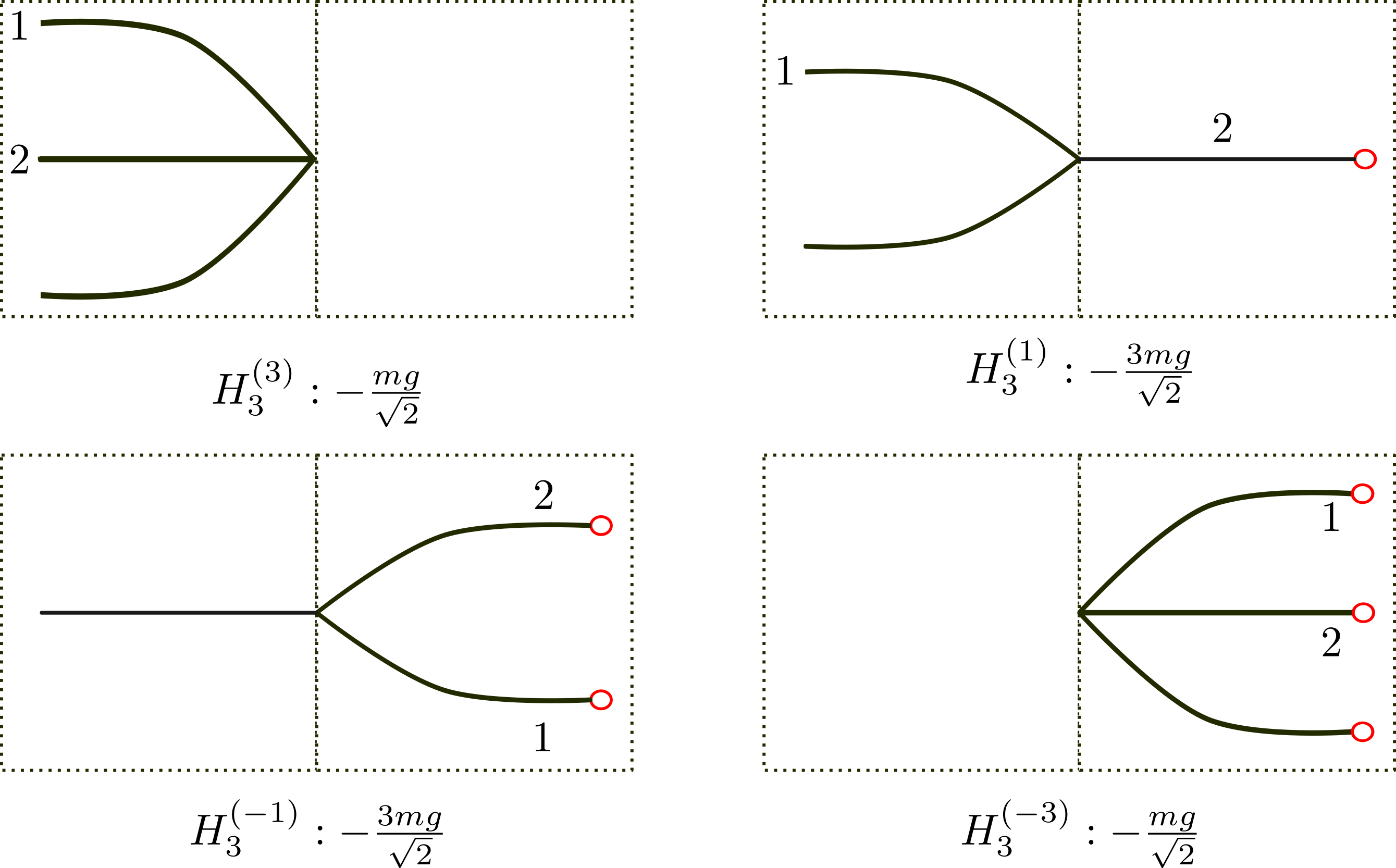
Rules for $H_ {3}^{(-)}$
Rules for $H_ {4}^{(-)}$
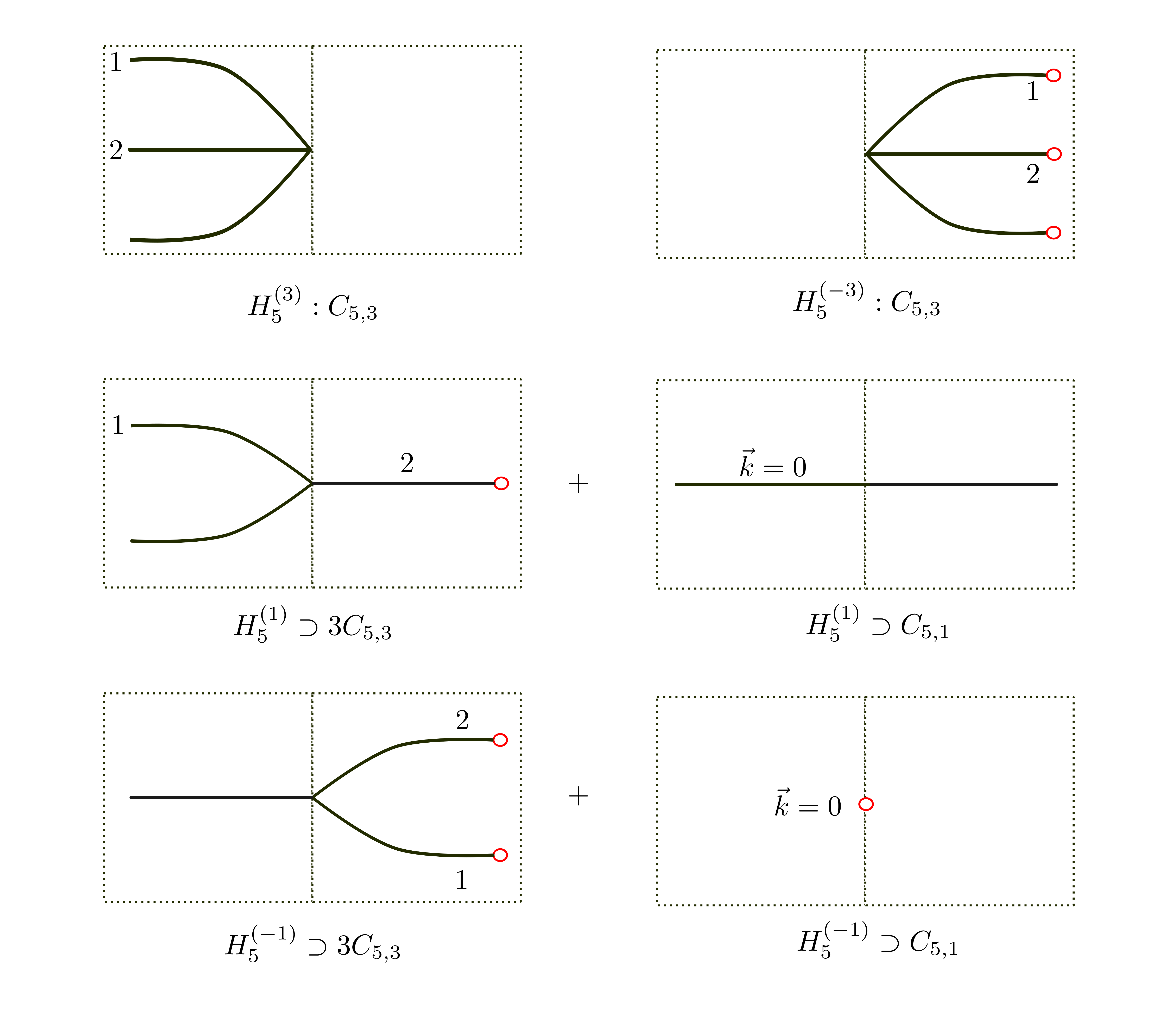
Rules for $H_ {5}^{(-)}$
Diagrams for States
Leading Order
At leading order there is one vacuum state correction and two momentum eigenstate corrections, their diagrammatic expressions are given in the figure below.

Next Leading Order
The fundamental diagrams for $\left\lvert \vec{p} \right\rangle_ {2}^{(-)}$ are shown in the below.
Let’s number the diagrams left to right, top to bottom. The contributions are
\[\begin{align*} (1) :\;& H_ {4}^{(4)} \left\lvert \vec{p} \right\rangle_ {0}^{(1)} = \frac{g^{2}}{4} \int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}} \, \left\lvert \vec{p},\vec{p}_ {1,2,3,-1-2-3} \right\rangle_ {0} , \\ (2) :\;& H_ {3}^{(3)} \left\lvert \vec{p} \right\rangle_ {1}^{(2)} = \frac{3g^{2}m^{2}}{4\omega_ {p}}\int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}} \, \frac{\left\lvert \vec{p}-\vec{p}_ {3}, \vec{p}_ {1,2,3,-1-2} \right\rangle_ {0}}{\omega _ {p}-\omega_ {3}-\omega_ {p-p_ {3}}} , \\ (3) :\;& H_ {3}^{(3)}\left\lvert \vec{p} \right\rangle_ {1}^{(4)} = -\frac{m^{2}g^{2}}{2} \int \frac{d^{3}p_ {1,2,3,4}}{(2\pi)^{12}} \, \frac{\left\lvert \vec{p},\vec{p}_ {1,2,3,4,-1-2,-3-4} \right\rangle_ {0}}{\omega_ {1}+\omega_ {2}+\omega_ {1+2}}, \\ (4) :\;& H_ {3}^{(1)} \left\lvert \vec{p} \right\rangle_ {1}^{(4)} \supset - \frac{3g^{2}m^{2}}{4} \int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}} \, \frac{3\left\lvert \vec{p},\vec{p}_ {1,2,3,-1-2-3} \right\rangle_ {0}}{\omega_ {2+3}(\omega_ {1}+\omega_ {2+3}+\omega_ {1+2+3})} , \\ (5) :\;& H_ {3}^{(1)}\left\lvert \vec{p} \right\rangle_ {1}^{(2)} = - \frac{9g^{2}m^{2}}{4\omega_ {p}} \int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}} \, \frac{\left\lvert \vec{p}-\vec{p}_ {1}-\vec{p}_ {2},\vec{p}_ {1,2} \right\rangle_ {0}}{\omega_ {1+2}(-\omega _ {p} +\omega_ {p-p_ {1}-p_ {2}}+\omega_ {1+2})} , \\ (6) :\;& H_ {3}^{(1)}\left\lvert \vec{p} \right\rangle_ {1}^{(4)} \supset - \frac{3g^{2}m^{2}}{4} \int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}} \, \frac{\left\lvert \vec{p}_ {1,2,3,-1-2},\vec{p}-\vec{p}_ {3} \right\rangle_ {0}}{\omega_ {p}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})} , \\ (7) :\;& H_ {3}^{(-1)}\left\lvert \vec{p} \right\rangle_ {1}^{(2)} = -\frac{9g^{2}m^{2}}{8\omega _ {p} } \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \frac{\left\lvert \vec{p} \right\rangle_ {0}}{\omega_ {1}\omega_ {p+p_ {1}}(-\omega _ {p} +\omega_ {1}+\omega_ {p+p_ {1}})}, \\ (8) :\;& H_ {3}^{(-1)}\left\lvert \vec{p} \right\rangle_ {1}^{(4)} \supset - \frac{9m^{2}g^{2}}{4\omega _ {p} } \int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}} \, \frac{\left\lvert \vec{p}-\vec{p}_ {1}-\vec{p}_ {2},\vec{p}_ {1,2} \right\rangle_ {0}}{\omega_ {1+2}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})} \\ (9) :\;& H_ {3}^{(-3)}\left\lvert p \right\rangle_ {1}^{(4)} \supset - \frac{3}{8}g^{2}m^{2}\left\lvert \vec{p} \right\rangle_ {0}\int d^{3}x \, \int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}} \, \frac{1}{\omega_ {1}\omega_ {2}\omega_ {1+2}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})} \\ (10) :\;& - H_ {3}^{(-3)}\left\lvert p \right\rangle_ {1}^{(4)} \supset \frac{9g^{2}m^{2}\left\lvert \vec{p} \right\rangle_ {0}}{8\omega _ {p} }\int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \frac{1}{\omega_ {1}\omega_ {p+p_ {1}}(\omega _ {p} +\omega_ {1}+\omega_ {p+p_ {1}})} \\ (11) :\;& H_ {3}^{(-1)}\left\lvert \vec{p} \right\rangle_ {1}^{(4)} \supset - \frac{9m^{2}g^{2}}{4} \int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}} \, \frac{\left\lvert \vec{p},\vec{p}_ {1,-1} \right\rangle_ {0}}{\omega_ {2}\omega_ {1+2}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})} \\ (12) :\;& H_ {4}^{(0)}\left\lvert p \right\rangle_ {0}^{(1)} \supset \int d^{3}x \, A_ {4}' ,\\ (13) : \;& H_ {4}^{(2)}\left\lvert p \right\rangle_ {0}^{(1)} \supset \frac{g^{2}}{2\omega _ {p} }\int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}} \, \left\lvert \vec{p}_ {1,2},\vec{p}-\vec{p}_ {1}-\vec{p}_ {2} \right\rangle, \\ (14) : \;& H_ {4}^{(2)}\left\lvert p \right\rangle_ {0}^{(1)} \supset - \frac{\delta m^{2}}{2}\int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \left\lvert \vec{p}_ {1,-1},\vec{p}\right\rangle ,\\ (15) : \;& H_ {4}^{(0)}\left\lvert p \right\rangle_ {0}^{(1)} \supset - \frac{\delta m^{2}}{4\omega p^{2}}\left\lvert \vec{p} \right\rangle. \end{align*}\]But in order to turn them into diagrammatic rules for corresponding Hilbert states. We need to inverse $(\omega _ {p}-H_ {2})$ to get components of $\left\lvert \vec{p} \right\rangle_ {2}$, eliminate the integral measures and deal with the creation operators. Note that the 1-meson states will eventually cancel out. Furthermore, we strip-off the propagators in the diagram since we are regarding them as a vertex as a whole, as shown below.

As diagrammatic rules we get:
\[\begin{align*} (1) :\;& H_ {4}^{(4)} \left\lvert \vec{p} \right\rangle_ {0}^{(1)} : -\frac{g^{2}}{4(\omega_ {1}+\omega_ {2}+\omega_ {3}+\omega_ {1+2+3})} , \\ (2) :\;& H_ {3}^{(3)} \left\lvert \vec{p} \right\rangle_ {1}^{(2)} :\frac{3g^{2}m^{2}}{4\omega_ {p}} \frac{1}{(-\omega _ {p}+\omega_ {3}+\omega_ {p-p_ {3}})(-\omega _ {p} +\omega_ {1}+\omega_ {2}+\omega_ {3}+\omega_ {1+2}+\omega_ {p-p_ {3}})} , \\ (3) :\;& H_ {3}^{(3)}\left\lvert \vec{p} \right\rangle_ {1}^{(4)}:\frac{m^{2}g^{2}}{2(\omega_ {1}+\omega_ {2}+\omega_ {1+2})(\omega_ {1}+\omega_ {2}+\omega_ {3}+\omega_ {4}+\omega_ {1+2}+\omega_ {3+4})}, \\ (4) :\;& H_ {3}^{(1)} \left\lvert \vec{p} \right\rangle_ {1}^{(4)} : \frac{9g^{2}m^{2}}{4\omega_ {2+3}(\omega_ {1}+\omega_ {2+3}+\omega_ {1+2+3})(\omega_ {1}+\omega_ {2}+\omega_ {3}+\omega_ {1+2+3})} , \\ (5) : \;& H_ {3}^{(1)}\left\lvert \vec{p} \right\rangle_ {1}^{(2)} : \frac{9g^{2}m^{2}}{4\omega_ {p}}\frac{1}{\omega_ {1+2}(-\omega _ {p} +\omega_ {p-p_ {1}-p_ {2}}+\omega_ {1+2})(-\omega _ {p} +\omega_ {1}+\omega_ {2}+\omega_ {p-p_ {1}-p_ {2}})} , \\ (6) :\;& H_ {3}^{(1)}\left\lvert \vec{p} \right\rangle_ {1}^{(4)} : \frac{3g^{2}m^{2}}{4\omega_ {p}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})(-\omega _ {p} +\omega_ {1}+\omega_ {2}+\omega_ {3}+\omega_ {1+2}+\omega_ {p-p_ {3}})} , \\ (8) :\;& H_ {3}^{(-1)}\left\lvert \vec{p} \right\rangle_ {1}^{(4)} : \frac{9m^{2}g^{2}}{4\omega _ {p} } \, \frac{1}{\omega_ {1+2}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})(-\omega _ {p} +\omega_ {p-p_ {1}-p_ {2}}+\omega_ {1}+\omega_ {2})}, \\ (11) :\;& H_ {3}^{(-1)}\left\lvert \vec{p} \right\rangle_ {1}^{(8)} : \frac{9m^{2}g^{2}}{8} \frac{1}{\omega_ {1}\omega_ {2}\omega_ {1+2}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})} ,\\ (13): \;& H_ {4}^{(2)}\left\lvert \vec{p} \right\rangle_ {0}^{(1)} : - \frac{g^{2}}{2\omega _ {p} } \frac{1}{(-\omega _ {p} +\omega_ {1}+\omega_ {2}+\omega_ {p-p_ {1}-p_ {2}})}, \\ (14): \;& H_ {4}^{(2)}\left\lvert \vec{p} \right\rangle_ {0}^{(1)} : \frac{\delta m^{2}}{4\omega_ {1}}. \end{align*}\]3rd Order States
Let’s start with momentum states.
$\left\lvert \vec{p} \right\rangle_ {3}^{(2)}:$
$H_ {3}^{(-3)}\left\lvert \vec{p} \right\rangle_ {2}^{(5)}$:
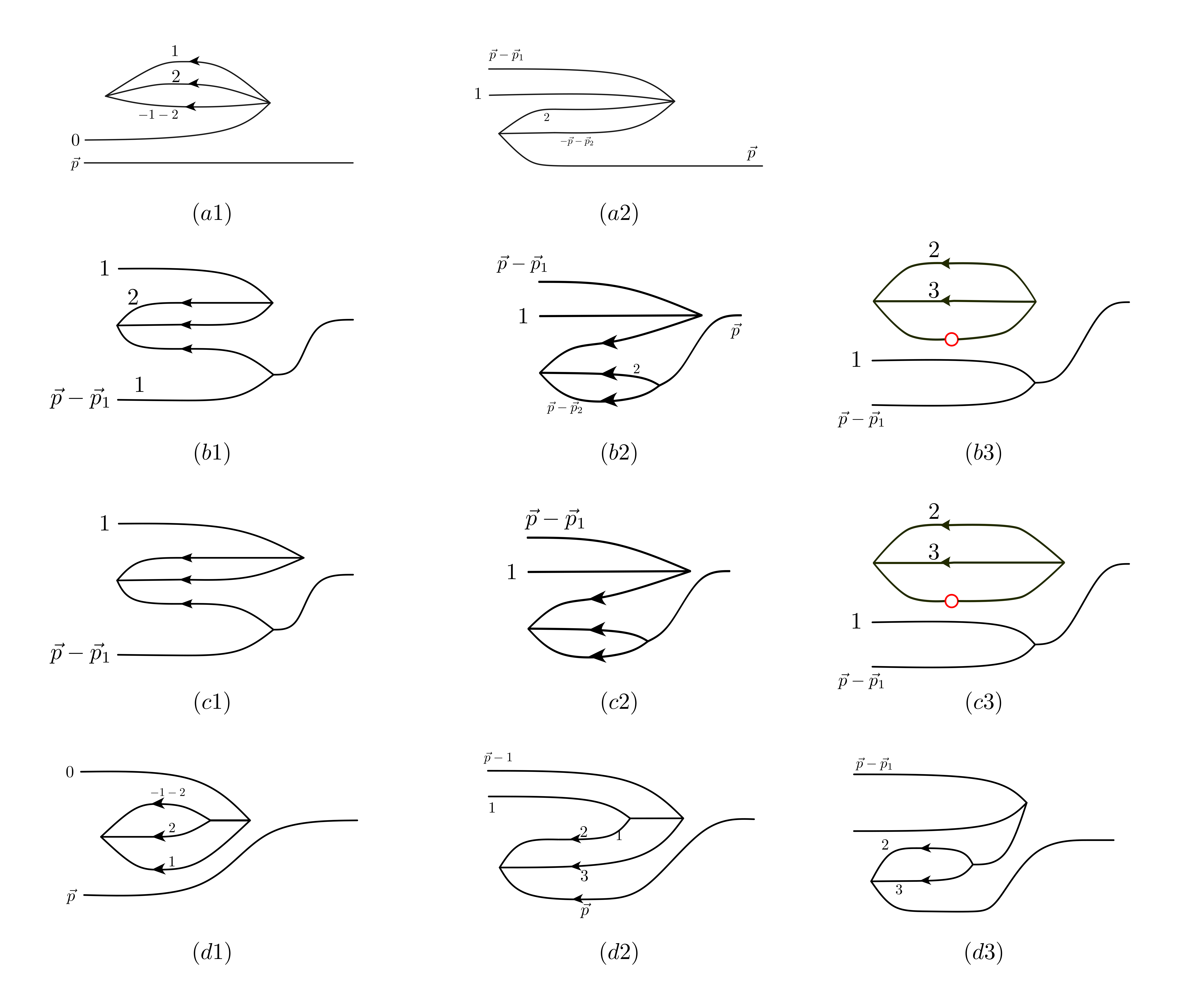
It includes four contributions: $H_ {3}^{(-3)}$ acting on panel (1), (2), (4) and (6) from figure 6.
The contributions $H_ {3}^{(-3)}\cdot(1)$ are shown in Figure 7 by panels (a1,a2). We have
\[\begin{align*} (a1) =& \frac{3mg^{3}}{4\sqrt{2}} \left\lvert \vec{p},0 \right\rangle \int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}} \, \frac{1}{\omega_ {1}\omega_ {2}\omega_ {1+2}(m+\omega_ {1}+\omega_ {2}+\omega_ {1+2})}, \\ (a2) =& \frac{9mg^{3}}{8\sqrt{2}\omega _ {p} } \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \left\lvert \vec{p}_ {1},\vec{p}-\vec{p}_ {1} \right\rangle \int \frac{d^{3}p_ {2}}{(2\pi)^{3}} \frac{1}{\omega_ {2}\omega_ {p+2}(\omega_ {1}+\omega_ {2}+\omega_ {p-1}+\omega_ {p+2})} . \end{align*}\]The components of $H_ {3}^{(-3)}\cdot(2)$ is shown in panel (b1,b2,b3):
\[\begin{align*} (b 1) =& - \frac{27m^{3}g^{3}}{8\sqrt{2}\omega _ {p} } \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \left\lvert \vec{p}_ {1},\vec{p}-\vec{p}_ {1} \right\rangle \int \frac{d^{3}p_ {2}}{(2\pi)^{3}} \, \frac{1}{\omega_ {1}\omega_ {2}\omega_ {1-2}} \\ & \times \frac{1}{(-\omega _ {p} +\omega_ {1}+\omega_ {p-p_ {1}})(-\omega _ {p}+2\omega_ {1} +\omega_ {2}+\omega_ {1+2}+\omega_ {p-p_ {1}})}, \\ (b 2) =& - \frac{27m^{3}g^{3}}{16\sqrt{2}\omega _ {p} ^{2}} \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \left\lvert \vec{p}_ {1},\vec{p}-\vec{p}_ {1} \right\rangle \int \frac{d^{3}p_ {2}}{(2\pi)^{3}} \, \frac{1}{\omega_ {2}\omega_ {p-p_ {2}}} \\ &\times \frac{1}{(-\omega _ {p} +\omega_ {2}+\omega_ {p-p_ {2}})(\omega_ {1}+\omega_ {2}+\omega_ {p-p_ {1}}+\omega_ {p-p_ {2}})} , \\ (b 3) =& - \frac{9m^{3}g^{3}}{16\sqrt{2}\omega _ {p} }\int d^{3}x \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \left\lvert \vec{p}_ {1},\vec{p}-\vec{p}_ {1} \right\rangle \int \frac{d^{3}p_ {2,3}}{(2\pi)^{6}} \, \frac{1}{\omega_ {2}\omega_ {3}\omega_ {2+3}} \\ &\times \frac{1}{(-\omega _ {p} +\omega_ {1}+\omega_ {p-p_ {1}})(-\omega _ {p} +\omega_ {1}+\omega_ {2}+\omega_ {3}+\omega_ {2+3}+\omega_ {p-p_ {1}})}. \end{align*}\]Next we calculate $H_ {3}^{(-3)}\cdot(4)$, given in panel (c1,c2,c3) in figure 6:
\[\begin{align*} (c 1) =& - \frac{81m^{3}g^{3}}{8\sqrt{2}} \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \left\lvert \vec{p}_ {1},\vec{p}-\vec{p}_ {1} \right\rangle \int \frac{d^{3} p_ {2}}{(2\pi)^{3}} \, \frac{1}{\omega_ {1}\omega_ {2}\omega^{2}_ {1+2}} \\ &\times \frac{1}{(\omega_ {1}+\omega_ {1+2}+\omega_ {2p_ {1}+2})(\omega_ {1}+\omega_ {1+2}+\omega_ {3}+\omega_ {2p_ {1}+2})},\\ (c 2) =& - \frac{81m^{3} g^{3}}{16\sqrt{2}} \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \left\lvert \vec{p},\vec{p}-\vec{p}_ {1} \right\rangle \int \frac{d^{3}p_ {2}}{(2\pi)^{3}} \, \frac{1}{\omega_ {2}\omega _ {p} \omega^{2}_ {p-2}} \\ &\times \frac{1}{(\omega_ {1}+\omega_ {2-p}+\omega_ {1+2-p})(\omega_ {1}+\omega_ {2}+\omega _ {p} +\omega_ {1+2-p})}, \\ (c 3) =& - \frac{27m^{3}g^{3}}{16\sqrt{2}} \int d^{3}x \, \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \left\lvert \vec{p},\vec{p}-\vec{p}_ {1} \right\rangle \int \frac{d^{3}p_ {2}}{(2\pi)^{3}} \, \frac{1}{\omega_ {2}\omega_ {3}\omega_ {2+3}} \\ &\times \frac{1}{\omega_ {1+2}(\omega_ {3}+\omega_ {1+2}+\omega_ {1+2+3})(\omega_ {1}+\omega_ {2}+\omega_ {3}+\omega_ {1+2+3})}. \end{align*}\]The contribution of $H_ {3}^{(-3)}\cdot(6)$, given in panel (d1,d2,d3):
\[\begin{align*} (d 1) =& - \frac{3m^{3}g^{3}\left\lvert \vec{p},0 \right\rangle}{4\sqrt{2}} \int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}} \, \frac{1}{\omega_ {1}\omega_ {2}\omega_ {1+2}\omega_ {p}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})} \\ &\times \frac{1}{(-\omega _ {p} +\omega_ {1}+\omega_ {2}+2\omega_ {1+2}+\omega_ {p-p_ {1}-p_ {2}})},\\ (d 2) =& - \frac{9m^{3}g^{3}}{4\sqrt{2}} \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \left\lvert \vec{p},\vec{p}-\vec{p}_ {1} \right\rangle \int \frac{d^{3}p_ {2,3}}{(2\pi)^{6}} \, \frac{1}{\omega_ {2}\omega_ {3}\omega^{2} _ {p} } \\ &\times \frac{1}{ (\omega_ {2}+\omega_ {3}+\omega_ {2+3})(-\omega _ {p} +\omega_ {1}+\omega_ {2}+\omega_ {3}+\omega_ {2+3}+\omega_ {p-p_ {1}})} ,\\ (d 3) =& - \frac{9m^{3}g^{3}}{4\sqrt{2}} \int \frac{d ^{3}p_ {1}}{(2\pi)^{3}} \, \left\lvert \vec{p},\vec{p}-\vec{p}_ {1} \right\rangle \int \frac{d^{3}p_ {2,3}}{(2\pi)^{6}} \, \frac{1}{\omega_ {2}\omega_ {3}\omega _ {p} ^{2}} \\ & \times \frac{1}{(\omega_ {1}+\omega_ {2}+\omega_ {1+2})(-\omega _ {p} +\omega_ {1}+\omega_ {2}+\omega_ {3}+\omega_ {1+2}+\omega _ {p-p_ {3}} )} . \end{align*}\]The diagrams are shown below.
$H_ {4}^{(0)}\left\lvert \vec{p} \right\rangle_ {1}^{(2)}:$
The diagrams are shown below.
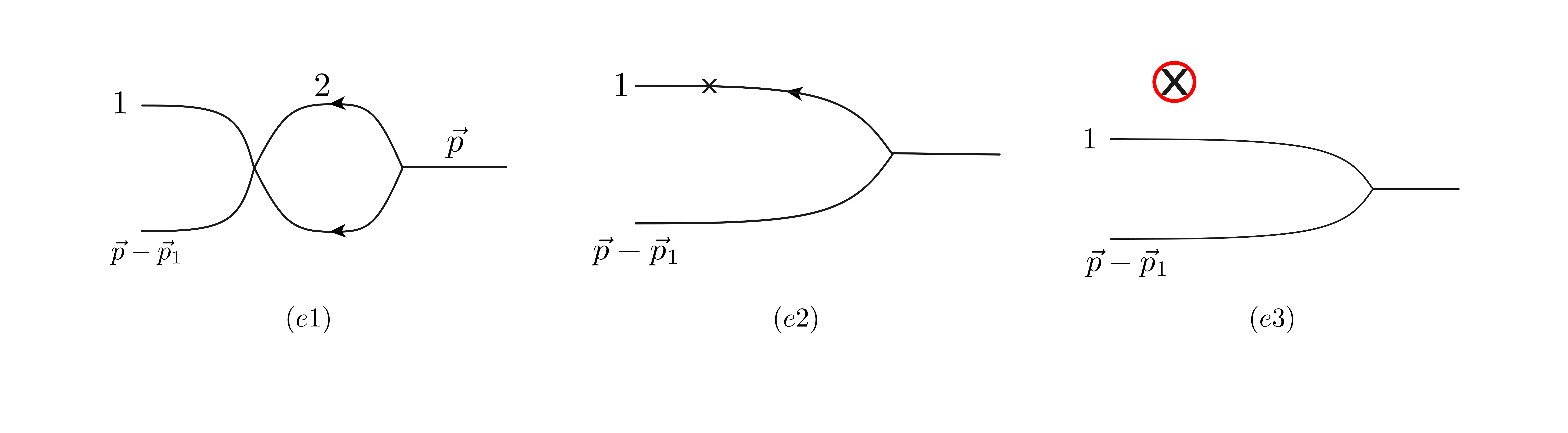
Their contributions correspondingly are
\[\begin{align*} (e 1) =& \frac{9mg^{3}}{8\sqrt{2}\omega _ {p} } \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \left\lvert \vec{p}_ {1},\vec{p}-\vec{p}_ {1} \right\rangle \int \frac{d^{3}p_ {2}}{(2\pi)^{3}} \, \frac{1}{\omega_ {2}\omega_ {p-2}(\omega _ {p} -\omega_ {2}-\omega_ {p-p_ {2}})} , \\ (e 2) =& -\frac{\delta m^{2} 3mg}{2\sqrt{2}\omega _ {p} }\int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \frac{\left\lvert \vec{p}_ {1}, \vec{p}-\vec{p}_ {1} \right\rangle}{\omega_ {1}(-\omega _ {p} +\omega_ {1}+\omega_ {p-p_ {1}})}, \\ (e 3) =& \frac{3A_ {4}'mg}{2\sqrt{2}\omega _ {p} }\int d^{3}x \, \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \frac{\left\lvert \vec{p},\vec{p}-\vec{p}_ {1} \right\rangle}{-\omega _ {p} +\omega_ {1}+\omega_ {p-p_ {1}}}. \end{align*}\]$H_ {3}^{(-1)}\left\lvert \vec{p} \right\rangle_ {2}^{(3)}:$
It includes three parts: $H_ {3}^{(-1)}$ acting on panel (5,8,11,13,14) in figure 6. The figure are shown below.
First of all, $H_ {3}^{(-1)}$ acting on panel (5). They correspond to panel (f1) and (f2) in figure 9 below.
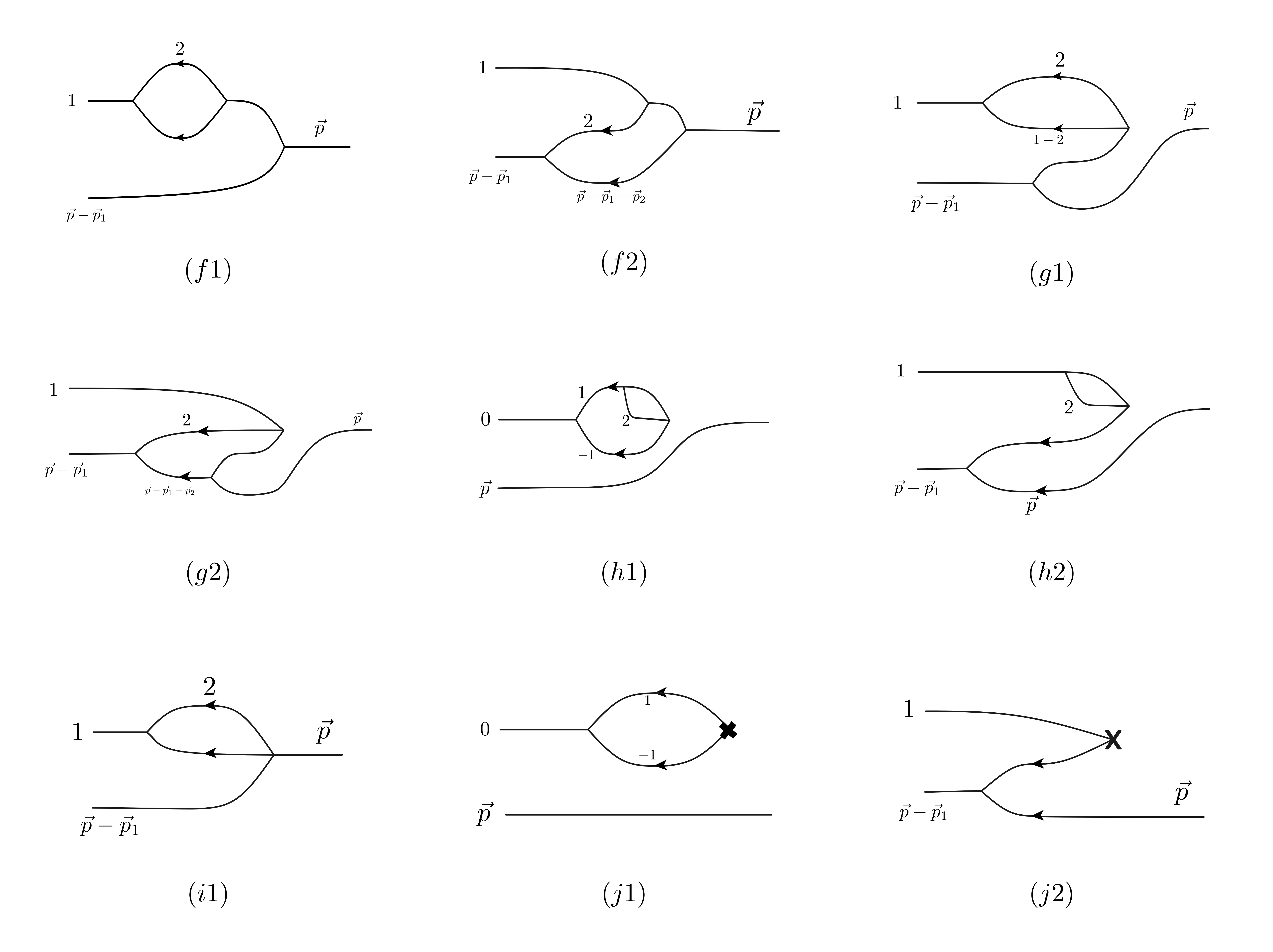
Their contributions are
\[\begin{align*} (f 1) =& - \frac{27g^{3}m^{3}}{8\sqrt{2}\omega _ {p} }\int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \left\lvert \vec{p}_ {1},\vec{p}-\vec{p}_ {1} \right\rangle \int \frac{d^{3}p_ {2}}{(2\pi)^{3}} \, \frac{1}{\omega_ {1}\omega_ {2}\omega_ {1-2}} \\ & \times \frac{1}{(-\omega _ {p} +\omega_ {1}+\omega_ {p-p_ {1}})(-\omega _ {p} +\omega_ {1}+\omega_ {2}+\omega_ {1-2})}, \\ (f 2) =& -\frac{27m^{3}g^{3}}{4\sqrt2\omega _ {p}} \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \left\lvert \vec{p}_ {1},\vec{p}-\vec{p}_ {1} \right\rangle \int \frac{d^{3}p_ {2}}{(2\pi)^{3}} \, \frac{1}{\omega_ {2}\omega_ {1+2}\omega_ {p-p_ {1}-p_ {2}}} \\ &\times \frac{1}{(-\omega _ {p} +\omega_ {p-p_ {1}-p_ {1}}+\omega_ {1+2})(-\omega _ {p} +\omega_ {1}+\omega_ {2}+\omega_ {p-p_ {1}-p_ {2}})}, \end{align*}\]Then we move on to $H_ {3}^{(-1)}$ acting on panel (8), given by panel (g1) and (g2) in figure 9. The contributions are
\[\begin{align*} (g 1) =& - \frac{27m^{3}g^{3}}{8\sqrt{2}\omega _ {p} } \int \frac{d^{3}p_ {1}}{(2\pi)^{3}}\left\lvert \vec{p}_ {1},\vec{p}-\vec{p}_ {1} \right\rangle \, \int \frac{d^{3}p_ {2}}{(2\pi)^{3}} \, \frac{1}{\omega_ {1}\omega_ {2}\omega_ {1-2}} \\ & \times \frac{1}{(\omega_ {1}+\omega_ {2}+\omega_ {1-2})(-\omega _ {p} +\omega_ {p-p_ {1}}+\omega_ {2}+\omega_ {1-2})}, \\ (g 2) =& - \frac{27m^{3}g^{3}}{4\sqrt{2}\omega _ {p} } \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \left\lvert \vec{p}_ {1},\vec{p}-\vec{p}_ {1} \right\rangle \int \frac{d^{3}p_ {2}}{(2\pi)^{3}} \, \frac{1}{\omega_ {2}\omega_ {1+2}\omega_ {p-p_ {1}-p_ {2}}} \\ & \times \frac{1}{(\omega_ {1}+\omega_ {2}+\omega_ {1+2})(-\omega _ {p} +\omega_ {1}+\omega_ {2}+\omega_ {p-p_ {1}-p_ {2}})}. \end{align*}\]Then $H_ {3}^{(-1)}$ acting on panel (11),given by panel (h1,h2):
\[\begin{align*} (h 1) =& - \frac{27m^{3}g^{3}}{16\sqrt{2}} \left\lvert \vec{p},0 \right\rangle \int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}} \, \frac{1}{\omega_ {1}^{3}\omega_ {2}\omega_ {1+2}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})}, \\ (h 2) =& - \frac{27m^{3}g^{3}}{8\sqrt{2}\omega _ {p} } \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \left\lvert \vec{p},\vec{p}-\vec{p}_ {1} \right\rangle \frac{1}{\omega_ {1}^{2}\omega_ {2}\omega_ {1+2}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})} . \end{align*}\]It looks weird that we have a $\left\lvert \vec{p}=0 \right\rangle$ state… it just pops out from the vacuum. Anyway, let’s move on.
$H_ {3}^{(-1)}$ acting on panel (13),given by panel (i1):
\[(i 1) = \frac{9mg^{3}}{4\sqrt{2}\omega _ {p} }\int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \left\lvert \vec{p}_ {1},\vec{p}-\vec{p}_ {1} \right\rangle \int \frac{d^{3}p_ {2}}{(2\pi)^{3}} \, \frac{1}{\omega_ {2}\omega_ {1-2}(-\omega _ {p} +\omega_ {2}+\omega_ {1-2}+\omega_ {p-p_ {1}})} ,\]and $H_ {3}^{(-1)}$ acting on panel (13) represented by panel (j1,j2), whose contributions are
\[\begin{align*} (j 1) =& - \frac{3\delta m^{2}m g}{32\sqrt{2}} \left\lvert \vec{p},0 \right\rangle \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \frac{1}{\omega^{3}_ {1}}, \\ (j 2) =& - \frac{3mg\delta m^{2}}{4\sqrt{2}\omega _ {p} } \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \frac{\left\lvert \vec{p}_ {1},\vec{p}-\vec{p}_ {1} \right\rangle}{\omega_ {1}^{2}}. \end{align*}\]$H_ {4}^{(-2)}\left\lvert \vec{p} \right\rangle_ {1}^{(4)}:$
This contribution is relatively simple, including one contribution only: $H_ {4}^{(-2)}$ acting on panel 3 in Figure 4. The diagrams are given in Figure 10, with contributions
\[\begin{align*} k 1=& \frac{3mg^{3}\left\lvert \vec{p},0 \right\rangle}{4\sqrt{2}} \int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}} \, \frac{1}{\omega_ {1} \omega_ {2} \omega_ {3}(\omega_ {1} + \omega_ {2} + \omega_ {1+2})} ,\\ k 2=& \frac{9 mg^{3}}{4\sqrt{2}\omega _ {p} } \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \left\lvert \vec{p},\vec{p}-\vec{p}_ {1} \right\rangle \int \frac{d^{3}p_ {2}}{(2\pi)^{3}} \, \frac{1}{\omega_ {2}\omega_ {1+2}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})} ,\\ \ell 1=& - \frac{3mg \delta m^{2} }{4\sqrt{2}} \left\lvert \vec{p},0 \right\rangle \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \frac{1}{\omega_ {1}^{2}(2\omega_ {1}+m)} ,\\ \ell 2=& - \frac{3mg \delta m^{2}}{4\sqrt{2}\omega^{2}_ {p} } \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \frac{\left\lvert \vec{p}_ {1},\vec{p}-\vec{p}_ {1} \right\rangle}{\omega_ {1}+\omega _ {p} +\omega_ {p-1}} . \end{align*}\]
Reducible Diagrams

Now we can sum up the previous results and organize diagrams according to their topology.
For the reducible diagrams we have
\[\begin{align*} H_ {4}^{(0)} \left\lvert \vec{p} \right\rangle_ {1}^{(2)} =& - \frac{3m\delta m^{2}g}{2\sqrt{2}\omega _ {p} }\int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \frac{\left\lvert \vec{p}_ {1}, \vec{p}-\vec{p}_ {1} \right\rangle_ {0}}{\omega_ {1}(-\omega _ {p} +\omega_ {1}+\omega_ {p+p_ {1}})},\\ H_ {3}^{(-1)}\left\lvert \vec{p} \right\rangle_ {1}^{(3)} =& - \frac{27m^{3}g^{3}}{8\sqrt{2}\omega _ {p} }\int \frac{d^{3}p_ {1}}{(2\pi^{3})} \, \frac{\left\lvert \vec{p}_ {1},\vec{p}-\vec{p}_ {1} \right\rangle_ {0}}{\omega_ {1}(-\omega _ {p} +\omega_ {1}+\omega_ { p-p_ {1}})} \\ &\times \int \frac{d^{3}p_ {2}}{(2\pi)^{3}} \, \frac{1}{\omega_ {1+2}\omega_ {2}(-\omega _ {p} +\omega_ {1+2}+\omega_ {2}+\omega_ {p-p_ {1}})}, \\ H_ {3}^{(-3)}\left\lvert \vec{p} \right\rangle_ {2}^{(5)} &= - \frac{27m^{3}g^{3}}{8\sqrt{2}\omega _ {p} }\int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \frac{\left\lvert \vec{p}_ {1}, \vec{p}-\vec{p}_ {1} \right\rangle}{\omega_ {1}(-\omega _ {p} +\omega_ {1}+\omega_ {p-p_ {1}})} \\ &\times \int \frac{d^{3}p_ {2}}{(2\pi)^{3}} \, \frac{1}{\omega_ {2}\omega_ {1+2}(-\omega _ {p} +2\omega_ {1}+\omega_ {2}+\omega_ {1+2}+\omega_ {p-p_ {1}})} \end{align*}\]Enjoy Reading This Article?
Here are some more articles you might like to read next: