Quantum Domain Wall in 4D Part II
Spontaneous Symmetry Breaking
Recall that the original, un-shifted Hamiltonian in terms of bare parameter, without normal ordering reads
\[\hat{\mathcal{H}}^{0}(\vec{x}) = \frac{1}{2}\pi^{2}(\vec{x})+\frac{1}{2} (\partial_ {i}\phi)^{2} - \frac{m_ {0}^{2}}{4} \phi^{2}(\vec{x}) + \frac{g_ {0}^{2}}{4} \phi^{4}(\vec{x}) + \gamma,\]It has two classical minima are obtained at $\pm \frac{m_ {0}}{\sqrt{ 2\lambda_ {0} }}$. As a result we have two degenerate vacua states $\left\lvert{0^{\pm}}\right\rangle$ satisfying
\[\left\langle{0^{-}}\right\rvert \phi \left\lvert{0^{-}}\right\rangle =- \frac{m_ {0}}{\sqrt{ 2\lambda_ {0} }},\quad \left\langle{0^{+}}\right\rvert \phi \left\lvert{0^{+}}\right\rangle =+ \frac{m_ {0}}{\sqrt{ 2\lambda_ {0} }}\]Now we want to study the quantum physics around one of the vacua, say $\left\langle \phi \right\rangle = \frac{m_ {0}}{\sqrt{ 2\lambda_ {0} }}$, and we want to apply perturbation methods, since it is usually the only way we know how to proceed. The question is how to do perturbation theory with Hamiltonian formalism? For the validation of perturbation method, the field fluctuation should be small, meaning $\left\langle \phi \right\rangle$ should be small, but it is clearly not the case here, since $m_ {0} / \sqrt{ 2 } g_ {0}$ is not small by any sense.
Another thing we need to keep in mind is the difference between bare and renormalized parameters, eventually we need to write down the observables in terms of not bare, but renormalized parameters. Following the philosophy of renormalized perturbative method, we should 1) separate the Hamiltonian into renormalized terms and counter terms, then 2) use the counter terms to cancel the divergence from loops, which are now written in terms of renormalized parameters. We wrote the vev of $\phi$ in terms of bare parameters, but that is only for pedagogical reasons, what we should really do it first write the Hamiltonian into the renormalized perturbation theory form,
\[\hat{\mathcal{H}} = \frac{1}{2}\pi^{2}(\vec{x})+\frac{1}{2} (\partial_ {i}\phi)^{2} - \frac{m^{2}}{4} \phi^{2}(\vec{x}) + \frac{\lambda}{4} \phi^{4}(\vec{x}) + A + \text{counter terms,}\]then look for the minimum of the double-well potential, now $\left\langle \phi \right\rangle = m / \sqrt{ 2 }g$, with out naught subscript.
The last but not the least thing we need to worry about is the normal ordering. So far my assumption is that, the Hamiltonian is defined at some intrinsic parameter $m_ {0}$, so the normal ordering should also be defined at $m_ {0}$; however, to make the calculation easier, we shift the normal ordering to another scale: $m$. We have already talked in length about how to perform this shift. The final result should not depend on the shift though.
In the context of Lagrangian formalism and path integral, the perturbation method is quite straightforward, we can redefine the field operator according to $\phi\to \frac{m }{\sqrt{ 2\lambda }}+\phi’$, so that the classical vacuum is obtained at $\phi’$ equals zero. The small fluctuation about $\frac{m }{\sqrt{ 2\lambda }}$ gives us the quantum effects, we will essentially calculate
\[Z[J] = \int D\phi' \, \exp \left\lbrace iS[\phi']+i \int \phi' J \right\rbrace ,\]but only include $\phi’\sim 0$.
How can we do the same thing but with Hamiltonian formalism? Anything that can be done with one formalism can equally be done in the other, it is just a matter of convenience.
The problem is, in Hamiltonian formalism and working with $\hat{\mathcal{H}}$, perturbation methods are just not applicable, because the expectation value $\left\langle \phi \right\rangle := \left\langle{0^{+}}\right\rvert \phi \left\lvert{0^{+}}\right\rangle$ is by no means a small quantity, in fact $\left\langle \phi \right\rangle$ scales as $1 / \sqrt{ \lambda }$, it actually blows up as $\lambda \to 0$. Then, similar to the Lagrangian case, we need to find some new field operator $\phi’$ such that $\left\langle \phi’ \right\rangle=0$, then we can study the effects of fluctuation of $\left\langle \phi’ \right\rangle$ perturbative in $\left\lvert{0^{+}}\right\rangle$ state. Turns out, $\phi’$ is connected to $\phi$ by a unitary transformation, and in the case at hand the unitary operator turns out to be the displacement operator $\mathcal{D}_ {v }$, where $v $ is some parameter to be determined. Note that we have replaced the arbitrary function $f(\vec{x})$ with a constant function $v $. We will explain it in the following.
Recall the defining property of displacement operator, $\mathcal{D}_ {f}^{\dagger}\phi \mathcal{D}_ {f}=\phi+f$. Thus if we let
\[\boxed{ v = -\frac{m }{\sqrt{ 2\lambda }} }\]then (at least at leading order)
\[\left\langle{0^{+}}\right\rvert \mathcal{D}_ {v }^{\dagger} \phi \mathcal{D}_ {v }\left\lvert{0^{+}}\right\rangle = \left\langle{0^{+}}\right\rvert \phi+v \left\lvert{0^{+}}\right\rangle = \frac{m }{\sqrt{ 2\lambda }}-\frac{m }{\sqrt{ 2\lambda }}=0,\]hence
\[\boxed{ 0=\left\langle{0^{+}}\right\rvert \phi'\left\lvert{0^{+}}\right\rangle, \quad \phi':= \mathcal{D}_ {v }^{\dagger}\phi \mathcal{D}_ {v }. }\]It inspires us to define a new Hamiltonian exactly in the same fashion,
\[\boxed{ \mathcal{H} := \mathcal{D}_ {v }^{\dagger} \hat{\mathcal{H}} \mathcal{D}_ {v }. }\]We are interested in the spectrum of the Hamiltonian. The good news is that, a unitary transformation preserves the spectrum! Now, in order to study the quantum correction, instead of working with $\hat{H}$, $\phi$ and $\left\lvert{0^{+}}\right\rangle$ where perturbative methods fail, we can work with $H, \phi’$ and $\left\lvert{0^{+}}\right\rangle$ where $\phi’$ can be dealt with perturbatively.
Remarks. Generally speaking, let $\mathcal{O}$ be any operator and $\left\lvert{\psi}\right\rangle$ its eigenstate. If $\mathcal{O}’=\mathcal{D}^{\dagger}\mathcal{O} \mathcal{D}$ is the unitary transformation of $\mathcal{O}$, then its eigenstate is $\mathcal{D}^{\dagger}\left\lvert{\psi}\right\rangle$, not $\left\lvert{\psi}\right\rangle$. It may seem weird to some people to team up $\mathcal{O}’$ and $\left\lvert{\psi}\right\rangle$, not $\mathcal{O}’$ and $\mathcal{D}^{\dagger}\left\lvert{\psi}\right\rangle$. In fact, it is exactly the point of our method! If we pair $\mathcal{O}’$ with $\mathcal{D}^{\dagger}\left\lvert{\psi}\right\rangle$ it would be a trivial transform compare to working with $\mathcal{O}$ and $\left\lvert{\psi}\right\rangle$, we will not get anything new! Paring up $\mathcal{O}’$ and $\left\lvert{\psi}\right\rangle$ makes it possible for perturbation methods. However, since $\left\lvert{\psi}\right\rangle$ is not the eigen state of $\mathcal{O}’$, it indeed raise some problems, the first and foremost is that now $\mathcal{O}’$ is probably not diagonalized in $\left\lvert{\psi}\right\rangle$, we need to find a way to diagonalized it. In our current case, since the displacement operator only shifts the operators by a constant, it actually preserves the diagonalization, meaning if $\hat{\mathcal{H}}$ is diagonalized in $\left\lvert{\psi}\right\rangle$’s then $\mathcal{D}^{\dagger} \hat{\mathcal{H}}\mathcal{D}$ is also diagonalized in $\left\lvert{\psi}\right\rangle$’s. But for a generic $\mathcal{D}_ {f}$ with non-trivial $f$, this will no longer be true. That would be the topic for the other half the the note, after we introduce the kink solution.
A comparison between displacement operator method to the case of regular functions might be helpful.
| Functions | QFT |
|---|---|
| A functions $f(x)$, a neighborhood about a special locus $x_ 0$ where the interesting things happen. | A Hilbert space, a quantum state $\left\lvert{\Psi}\right\rangle$ of interest represented by a functional $\left\langle \Psi(x),- \right\rangle$, and some operator $\mathcal{O}(\phi)$. |
| We want to study the function $f(x )$ about $x_ 0$ perturbatively, | We want to study the $\left\langle{\Psi}\right\rvert\mathcal{O}\left\lvert{\Psi}\right\rangle$ perturbatively, |
| but $x_ 0$ is not a small quantity so Maclaurin expansion (Taylor expansion at the origin) fails. | but $\left\langle{\Psi}\right\rvert\phi \left\lvert{\Psi}\right\rangle=:f(x)$ is too large for $\phi$ to be treated perturbatively. |
| In a passive perspective, we shift the origin to $x_ 0$, then small deviation from $x_ 0$ can now be studied using Maclaurin expansion perturbatively. | In a passive perspective, we shift the operators, especially the field operator $\phi$ since it is usually the building block of other operators. The expectation value of the new, shifted operator $\phi’$ should be zero, $\left\langle{\Psi}\right\rvert \phi’\left\lvert{\Psi}\right\rangle =0$. Now we can treat $\phi$ perturbatively. |
| We are using a new, shifted coordinate system $\left\lbrace \overline{x} \right\rbrace$ to study the same old functions $f(x)$. | We are using shifted operators $\mathcal{D}^{\dagger}\mathcal{O}\mathcal{D}$ to study the same old states $\left\lvert{\Psi}\right\rangle$. |
In summary, now $\mathcal{H}=\mathcal{D}^{\dagger}_ {v}\hat{\mathcal{H}}\mathcal{D}_ {v}$ is a operator-valued function of $\phi’ = \mathcal{D}_ {v}^{\dagger} \phi \mathcal{D}_ {v}$, and $\phi’$ can be dealt with perturbatively. For the value of $v$, we could choose it to be the bare parameter or renormalized parameter, the final result should not depend on the convention we choose, in our note, in the spirit of renormalized perturbation theory, we choose $v$ to be renormalized, the associated displacement operator is $\mathcal{D}_ {v}$. Still, $v$ receives quantum corrections order by order, the full expression for $v$ would be an expansion in $g$:
\[v = -\frac{m}{\sqrt{ 2 }g} +\delta v, \quad \delta v = \delta v_ {1}+\delta v_ {2}+\cdots, \quad \delta v_ {i} \sim \mathcal{O}(g^{i}).\]In renormalized parameters the Hamiltonian reads (up to $\mathcal{O}(g^{3})$)
\[\begin{align*} \hat{H}(\vec{x}) &\supset \int d^{3}x \, : \frac{1}{2}\pi^{2}+\frac{1}{2}(\partial_ {i}\phi)^{2} - \frac{m^{2}}{4}\phi^{2}+\frac{g^{2}}{4}\phi^{4}:_ {m} \\ &\;\;\;\; + \int d^{3}x \, : \frac{\delta m^{2}}{4}\phi^{2}-\frac{1}{2}g \delta g\phi^{4} + \frac{(\delta g)^{2}}{4}\phi^{4} + \frac{3}{2}(g-\delta g)^{2}I\phi^{2}-\frac{3}{4}m^{2}I +A :_ {m}. \end{align*}\]Recall that $I$ is some integral of higher order of the coupling, we defined it in part I of the note. We need to sandwich the Hamiltonian by $\mathcal{D}_ {v}$ to get the shifted Hamiltonian density $\mathcal{H}$. We will expand $\mathcal{H}$ in power of $g=\sqrt{ \lambda }$. With some help from Mathematica, we find the following results.
\[\begin{align*} \mathcal{H}_ {0} &= A_ 0-\frac{m^4}{16 g^2}, \\ \mathcal{H}_ {1} &= A_ {1} \equiv 0, \\ \mathcal{H}_ {2} &= \frac{\pi^{2}}{2} + \frac{(\partial \phi)^{2}}{2} + \frac{m^{2}\phi^{2}}{2} + \frac{m^{4}}{8g^{2}}\left( -\frac{\delta g}{g} + \frac{\delta m^{2}_ {1}}{m^{2}} + \frac{\delta m^{4}_ {1}}{8g^{2}} \right) + A_ {2}, \\ \mathcal{H}_ {3} &= - \frac{mg}{\sqrt{ 2 }} \phi^{3} + \phi\left( m^{2}\delta v_ {1}+\frac{m^{3}}{\sqrt{ 2 }g} \left( \frac{\delta g}{g} - \frac{\delta m^{2}_ {1}}{2m^{2}} - \frac{\delta m^{4}_ {1}}{2g^{2}} \right) \right) + A_ {3}, \\ \mathcal{H}_ {4} &= \frac{g^{2}}{4}\phi^{4} + \phi^{2}\left( - \frac{3gm\delta v_ {1}}{\sqrt{ 2 }} - \frac{3m^{2}\delta g}{2g} + \frac{\delta m^{2}_ {1}}{4} + \frac{3m^{2}\delta m_ {1}^{4}}{4g^{2}} \right)+ \phi(m^{2}\delta v_ {2}) \\ &\;\;\;\; + \frac{m^{4}(\delta g)^{2}}{16g^{4}} + \frac{m^{3}\delta v_ {1}}{\sqrt{ 2 }g}\left( \frac{g}{\sqrt{ 2 }m} \delta v_ {1} + \frac{\delta g_ {1}}{g} - \frac{\delta m_ {1}^{2}}{2m^{2}} - \frac{\delta m_ {1}^{4}}{2g^{2}} \right) + A_ 4, \\ \mathcal{H}_ {5} &= \phi^{3}\left( g^{2}\delta v_ {1}+\sqrt{2}m\delta g_ {1}- \frac{m\delta m_ {1}^{4}}{\sqrt{2}g} \right) - \phi^{2}\left( \frac{3mg \delta v_ {2}}{\sqrt{2}} \right) \\ &\;\;\;\; + \phi\left( m^{2}\delta v_ {3} - \frac{3gm\delta v_ {1}^{2}}{\sqrt{2}} - \frac{3m^{2}\delta g_ {1}\delta v_ {1}}{g} - \frac{m^{3}(\delta g)^{2}}{2\sqrt{2}g^{3}} + \frac{1}{2}\delta m_ {1}^{2}\delta v_ {1} - \frac{3mg I_ {1}}{\sqrt{2}} + \frac{3m^{2}\delta m_ {1}^{4}\delta v_ {1}}{2g^{2}} \right) \\ &\;\;\;\; + \frac{m^{3}\delta v_ {2}}{\sqrt{2}g}\left( \frac{\delta g}{g} - \frac{\delta m_ {1}^{2}}{2m^{2}} - \frac{\delta m_ {1}^{4}}{2g^{2}} + \frac{\sqrt{2}g\delta v_ {1}}{m} \right) + A_ {5}. \end{align*}\]Hamiltonian Renormalization
The wavefunctions are expanded as
\[\begin{align*} \left\lvert{\Psi}\right\rangle &= \left\lvert{\Psi_ {0}}\right\rangle + \left\lvert{\Psi_ {1}}\right\rangle + \cdots = \sum_ {i=0}^{\infty} \left\lvert{\Psi_ {i}}\right\rangle , \\ \left\lvert{\Psi _ {i} }\right\rangle &\sim g^{i}. \end{align*}\]The Hamiltonian renormalization conditions (HRC) are as follows.
- Vacuum condition: $H\left\lvert{\Psi}\right\rangle=0$ at all orders.
- Theory is defined at mass $m$: $H\left\lvert{\vec{p}}\right\rangle = \omega_ {p,m}\left\lvert{\vec{p}}\right\rangle$. We will just neglect $m$.
- $_ {0}\left\langle \vec{p}_ {1}\vec{p}_ {2} \middle\vert \vec{p}\right\rangle_ {i\geq2}=0$,
- No tadpole, $\left\langle{\Omega}\right\rvert\phi \left\lvert{\Omega}\right\rangle=0$.
These are non-perturbative conditions, meaning they apply to all the orders, and the states involved are in general non-perturbative states, they can be expanded order by order. $\left\lvert{\Omega}\right\rangle$ is the full vacuum state with interaction, sometimes called physical vacuum. $\left\lvert{\vec{p}_ {1}\cdots\vec{p}_ {n}}\right\rangle$ is an $n$-meson momenta eigenstate. We define the leading order of the vacuum to be:
\[A_ {p} \left\lvert{\Omega_ {0}}\right\rangle =0.\]Similarly $\left\lvert{\vec{p}}\right\rangle$ is the full momentum eigenstate, $\left\lvert{\vec{p}}\right\rangle=\left\lvert{\vec{p}_ {0}}\right\rangle + \left\lvert{\vec{p}_ {1}}\right\rangle+\cdots$. Recall that in the interaction picture we have $\left\lvert{\vec{p}}\right\rangle=\frac{a^{\dagger}}{\sqrt{2\omega_ {p,m}}}\left\lvert{0}\right\rangle$, it is because in the interaction picture the operator $\phi$ is exactly solvable, the solution is by construction the same as if interaction does not exist. However we are working in Schrodinger picture, so this simple relation only holds at leading order,
\[\left\lvert{\vec{p}}\right\rangle_ {0} = A^{\ddagger}_ {p}\left\lvert{\Omega_ {0}}\right\rangle .\]The non-perturbative definition, $H\left\lvert{\vec{p}}\right\rangle=\vec{p}\left\lvert{\vec{p}}\right\rangle$, holds at each and every order.
The orthonormal conditions are:
\[\begin{align*} \left\langle \Omega_ {0} \middle\vert \Omega_ {0} \right\rangle &= 1,\\ \left\lvert{\vec{p}_ {1}\cdots \vec{p}_ {n} }\right\rangle_ {0} &= A^{\ddagger}_ {p_ {1}}\cdots A^{\ddagger}_ {p_ {n} }\left\lvert{\Omega_ {0}}\right\rangle . \end{align*}\]In this note I will use $\left\lvert{\Omega_ {i}}\right\rangle$ and $\left\lvert{\Omega}\right\rangle_ {i}$ interchangeably.
The first Hamiltonian renormalization condition (HRC) is expanded to
\[\boxed{ H\left\lvert{\Omega}\right\rangle = \sum_ {i}^{\infty}H_ {i=0} \sum_ {j=0}^{\infty} \left\lvert{\Omega _ {j} }\right\rangle = \sum_ {i,j=0}^{\infty} H_ {i} \left\lvert{\Omega _ {j} }\right\rangle\sim g^{i+j-2}. }\]The non-perturbed Fock states consists a full basis of Hilbert space, the $n$-meson states is defined to be
\[\left\lvert{\vec{p}_ {1}\cdots\vec{p}_ {n}}\right\rangle_ 0 := A_ {p_ {1}}^{\ddagger}\cdots A_ {p_ {n} }^{\ddagger} \left\lvert{\Omega_ {0}}\right\rangle .\]We will use them to expand states of higher order in $g$, for example $\left\lvert{\Omega_ {n}}\right\rangle$ is the $g^{n}$-order vacuum correction, we will expand it as
\[\left\lvert{\Omega_ {n}}\right\rangle = \sum_ {i=0}^{\infty} \left\lvert{\Omega_ {n}}\right\rangle^{(i)} , \quad \left\lvert{\Omega}\right\rangle^{(i)} \in i\text{-meson Fock space.}\]We have two things to match: 1)different orders of the coupling and 2)different Fock space.
Order $g^{-2}$ and $g^{-1}$
At the lowest order, the Hamiltonian density is just a constant without ladder operators, so $H_ {0}\left\lvert{\Omega_ {0}}\right\rangle=0$ gives as $\mathcal{H}_ {0}=0$, which implies $A_ {0} = m^{4} / 16g^{2}$.
By construction we have $H_ {1}=0$.
Take away:
\(\boxed{ H_ {0}=H_ {1}=0. }\)
Order $g^{0}$
The first HRC (HRC1), namely $H\left\lvert{\Omega}\right\rangle=0$ implies that
\[H_ {2}\left\lvert{\Omega_ {0}}\right\rangle = 0 ,\]which in turn implies
\[A_ {2} = - \frac{m^{4}}{8g^{2}} \left( -\frac{\delta g}{g} + \frac{\delta m_ {1}^{2}}{m^{2}}+ \frac{\delta m_ {1}^{4}}{\delta g^{2}} \right),\]as a result
\[\begin{align*} \mathcal{H}_ {2} &= \frac{\pi^{2}}{2} + \frac{(\partial \phi)^{2}}{2} + \frac{1}{2}m^{2}\phi^{2},\\ H_ {2} &=\int d^{3}x \, : \mathcal{H}_ {2} :_ {m} = \int \frac{d^{3}p}{(2\pi)^{3}} \, \omega_ {p} A^{\ddagger}_ {p} A_ {p} . \end{align*}\]Order $g^{1}$
Similar to order $g^{0}$, HRC1 implies that
\[H_ {2}\left\lvert{\Omega_ {1}}\right\rangle = -H_ {3} \left\lvert{\Omega_ {0}}\right\rangle . \tag{HRC1}\]Now we need to expand $\left\lvert{\Omega_ {1}}\right\rangle$ in $\left\lvert \Omega_ {0} \right\rangle$ and free field Fock states. Such state are created by free creation operators acting on free vacuum state,
\[\left\lvert \vec{p} \right\rangle_ {0} = A^{\ddagger}_ {p} \left\lvert \Omega_ {0} \right\rangle\]and
\[\left\lvert \vec{p}_ {1}\cdots \vec{p}_ {n} \right\rangle_ {0} = A_ {p_ {1}}^{\ddagger}\cdots A^{\ddagger}_ {p_ {n} }\left\lvert \Omega_ {0} \right\rangle .\]What is the norm of $\left\lvert \vec{p} \right\rangle_ {0}$? We have $_ {0}\left\langle \vec{p} \right\rvert=\left\langle \Omega_ {0} \right\rvert (A_ {p}^{\ddagger})^{\dagger}=\left\langle \Omega_ {0} \right\rvert(A_ {p})/2\omega_ {p}$ and $[A_ {p},A^{\ddagger}q]=(2\pi)^{3} \delta^{3}(\vec{p}-\vec{q})$, thus
\[\boxed{ _ {0}\left\langle \vec{p} \middle\vert \vec{q} \right\rangle_ {0} = \frac{(2\pi)^{3}}{2\omega _ {p} } \delta^{(3)}(\vec{p}-\vec{q}). }\]The free Fock states consist a full basis of Hilbert space. We can expand the first order correction to the vacuum states in these basis,
\[\left\lvert{\Omega_ {1}}\right\rangle = \left\lvert{\Omega_ {1}^{(0)}}\right\rangle + \left\lvert{\Omega_ {1}^{(1)}}\right\rangle + \cdots\]where $\left\lvert{\Omega_ {1}^{(0)}}\right\rangle$ isthe same as $\left\lvert{\Omega_ {1}}\right\rangle^{(0)}$, the superscript indicates the number of mesons, $\left\lvert \Omega_ {1}^{(n)} \right\rangle$ means the $n$-meson Fock space component of $\left\lvert \Omega_ {1} \right\rangle$ state. Explicitly we have
\[\left\lvert{\Omega^{(0)}_ {1}}\right\rangle = c_ {1,0} \left\lvert \Omega_ {0} \right\rangle , \quad c_ {1,0}\in \mathbb{C}.\]I will assume that $c_ {1,0}=0$, which is quite reasonable since the correction should be something new. And
\[\left\lvert \Omega_ {1}^{(1)} \right\rangle = \sum c_ {1,i} \left\lvert p_ {i} \right\rangle_ 0 , \quad c_ {1,i}\in \mathbb{C}.\]Generalizing it to multi-meson Fock space, we have
\[\left\lvert \Omega_ {1}^{(n)} \right\rangle =\sum_ {I} c_ {1,I} \left\lvert p_ {I} \right\rangle , \quad I = i_ {1}\cdots i_ {n},\; n>1,\]where $I$ is the general index, $\left\lvert p_ {I} \right\rangle=\left\lvert p_ {i_ {1}}p_ {i_ {2}}\cdots p_ {i_ {n}} \right\rangle$.
Are states from different Fock spaces orthogonal to each other? It will look something like
\[_ {0}\left\langle \vec{p}_ {I} \middle\vert \vec{p}_ {J} \right\rangle_ {0} \propto \left\langle \Omega_ {0} \right\rvert A\cdots A A^{\ddagger}\cdots A^{\ddagger}\left\lvert \Omega \right\rangle .\]According to the equal-time Wick theorem, a string of ladder operators is equal to the normal ordering of all its contraction, which, when sandwiched between vacuum state, can only be non-zero if it is a full contraction, where there are equal number of creation and annihilation operators. It means that these two states must
have same number of particles in it, hence belong to the same order of Fock subspace. Thus
\[\left\langle \Psi^{(m)} \middle\vert \Psi^{(n)} \right\rangle =0 \text{ if } m \neq n.\]Coming back to $\left\lvert \Omega_ {1} \right\rangle$. Focusing on the $0$-meson sub Fock space, we have
\[H_ {2}\left\lvert{\Omega_ {1}}\right\rangle \supset H_ {2}(\cdots)\left\lvert{\Omega_ {0}}\right\rangle =0,\]since $H_ {2}$ is normal ordered. On the right hand side, the zero-meson part of $-H_ {3}\left\lvert \Omega_ {0} \right\rangle$ is what? $H_ {3}$ can be written as
\[H_ {3} = \int d^{3}x \, :- \frac{mg}{\sqrt{2}} \phi^{3}+\phi m^{2} \delta v_ {1}' + A_ {3} :_ {m},\]where $\delta v_ {1}’$ is some function of counter terms. Thanks to the normal ordering, in $0$-Fock subspace we have
\[0\text{-meson:}\quad H_ {3}\left\lvert \Omega_ {0} \right\rangle =A_ {3}\left\lvert \Omega_ {0}\right\rangle=0 \implies A_ {3}=0 .\]To study what is going on with multi-mesons states, we need to expand the Hamiltonians $H_ {2}$ and $H_ {3}$ in ladder operators. According to the convention we introduced in the first part of the note, we have
\[H_ {2} = \int \frac{d^{3}p}{(2\pi)^{3}} \, \omega_ {p} A^{\ddagger}_ {p} A_ {p} .\]Let $(123)$ be the permutation action that maps 1st element to 2nd, 2nd to 3rd, and 3rd to 1st, we have
\[\begin{align*} H_ {3} = &-\frac{mg}{\sqrt{2}} \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \frac{d^{3}p_ {2}}{(2\pi)^{3}}\, \bigg\{ A_ {p_ {1}}^{\ddagger}A_ {p_ {1}}^{\ddagger}A_ {p_ {3}}^{\ddagger} \\ &+ \frac{1}{2\omega_ {p_ {3}}}A_ {p_ {1}}^{\ddagger}A_ {p_ {2}}^{\ddagger}A_ {-p_ {3}} + (123)+(123)^{2} \\ &+\frac{1}{2\omega_ {p_ {2}}} \frac{1}{2\omega_ {p_ {3}}} A_ {p_ {1}}^{\ddagger}A_ {-p_ {2}} A_ {-p_ {3}} + (123)+(123)^{2} \\ & + \left.\frac{1}{2\omega_ {p_ {1}}2\omega_ {p_ {2}}2\omega_ {p_ {3}}} A_ {-p_ {1}}A_ {-p_ {2}}A_ {-p_ {3}} \right\rbrace \\ &+ m^{2}\delta v_ {1}'\left( A^{\ddagger}_ {p=0}+\frac{A_ {p=0}}{2m} \right), \\ p_ {3} =& -p_ {1}-p_ {2},\\ \delta v_ {1}' =& \delta v_ {1}+\frac{m}{\sqrt{2}g} \left( \frac{\delta g}{g} - \frac{\delta m^{2}_ {1}}{2m^{2}} - \frac{\delta m^{4}_ {1}}{2g^{2}}\right). \end{align*}\]In order to solve the order $g$ HRC1 equation
\[H_ {2}\left\lvert{\Omega_ {1}}\right\rangle = -H_ {3} \left\lvert{\Omega_ {0}}\right\rangle\]for $\left\lvert \Omega_ {1} \right\rangle$, we would like to find the inverse of $H_ {2}$. The kernel of $H_ {2}$ is $\left\lvert \Omega_ {0} \right\rangle$, of course inverse of $H_ {2}$ does not exist on $\left\lvert \Omega_ {0} \right\rangle$. But we can always define the inverse on other Fock states. For example, consider a 3-meson state $\left\lvert \vec{p}_ {1}\vec{p}_ {2}\vec{p}_ {3} \right\rangle_ {0}$, since $H_ {2}$ is diagonalized in these basis, the inverse can be trivially written as $\frac{1}{H_ {2}}$ where $H_ {2}$ is to be understood as its eigenvalues,
\[\frac{1}{ H_ {2}} \left\lvert \vec{p}_ {1}\vec{p}_ {2}\vec{p}_ {3} \right\rangle_ {0} = \frac{1}{\omega_ {p_ {1}}\omega_ {p_ {2}}\omega_ {p_ {3}}} \left\lvert \vec{p}_ {1}\vec{p}_ {2}\vec{p}_ {3} \right\rangle_ {0}.\]Since we have established that $\left\lvert \Omega_ {1} \right\rangle$ does not contain $\Omega_ {0}$ component, that is $\Omega_ {1}$ does not contain the kernel of $H_ {2}$, we can write formally
\[\left\lvert \Omega_ {1} \right\rangle = - \frac{1}{H_ {2}} H_ {3} \left\lvert \Omega_ {0} \right\rangle\]Substitute the expression for $H_ {3}$, we have (after some trivial rearrangement)
\[\begin{align*} \left\lvert \Omega_ {1} \right\rangle =& \frac{mg}{\sqrt{2}} \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \frac{d^{3}p_ {2}}{(2\pi)^{3}} \, \frac{\left\lvert \vec{p}_ {1}\vec{p}_ {2}\vec{p}_ {3} \right\rangle_ {0} }{(\omega_ {p_ {1}}+\omega_ {p_ {2}}+\omega_ {p_ {3}})} \\ &- m\delta v_ {1}' \left\lvert \vec{p}=0 \right\rangle_ {0} ,\\ \vec{p}_ {3} =& -\vec{p}_ {1}-\vec{p}_ {2}. \end{align*}\]The no-tadpole rule demands that $\left\langle \Omega \right\rvert\phi \left\lvert \Omega \right\rangle=0$, expand $\left\lvert \Omega \right\rangle$ up to $\left\lvert \Omega_ {1} \right\rangle$ we get
\[\begin{align*} \left\langle \Omega \right\rvert \phi \left\lvert \Omega \right\rangle &= (\left\langle \Omega_ {0} \right\rvert +\left\langle \Omega_ {1} \right\rvert ) \phi (\left\lvert \Omega_ {0} \right\rangle +\left\lvert \Omega_ {1} \right\rangle ) \\ &= 2 \left\langle \Omega_ {0} \right\rvert \int \frac{d^{3}k}{(2\pi)^{3}} \, e^{ -i\vec{k}\cdot \vec{x} } \frac{A_ {-k}}{2\omega_ {k}} (-m\delta v_ {1}')A^{\ddagger}_ {p=0} \left\lvert \Omega_ {0} \right\rangle \\ &= -\delta v_ {1}'\\ &=0. \end{align*}\]The long-ass expression for $\delta v_ {1}’$ turns out to be zero. This can be translated into a relation for $\delta v_ {1}$, which will help us to simplify the higher order Hamiltonians:
\[\boxed{ \delta v_ {1}=- \frac{m}{\sqrt{2}g} \left( \frac{\delta g}{g}- \frac{\delta m_ {1}^{2}}{2m^{2}}- \frac{\delta m_ {1}^{4}}{2g^{2}} \right). }\]Putting everything together, we find
\[\boxed{ \mathcal{H}_ {3}(\vec{x}) = -\frac{mg}{\sqrt{2}} \phi^{3}(\vec{x}), }\]everything else has disappeared. The first order correction to vacuum state is
\[\boxed{ \left\lvert \Omega_ {1} \right\rangle = \frac{mg}{\sqrt{2}} \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \frac{d^{3}p_ {2}}{(2\pi)^{3}} \, \frac{\left\lvert \vec{p}_ {1}\vec{p}_ {2}\vec{p}_ {3} \right\rangle_ {0} }{(\omega_ {p_ {1}}+\omega_ {p_ {2}}+\omega_ {p_ {3}})}, \quad \vec{p}_ {1}+\vec{p}_ {2}+\vec{p}_ {3}=0 }\]We are not quite done yet, we need to find the interaction correction to the momentum eigenstates. At lowest order we have $H_ {0}\left\lvert \vec{p} \right\rangle_ {0}=\omega_ {p}\left\lvert \vec{p} \right\rangle_ {0}$, and after we include all orders we require that $H\left\lvert \vec{p} \right\rangle=\omega_ {p}\left\lvert p \right\rangle$. Our task is to find the difference between $\left\lvert - \right\rangle_ {0}$ and $\left\lvert - \right\rangle$ order by order.
In order to make it easier to keep tracks of the number of mesons, let’s introduce the following notation.
- For a state, we use a superscript in parenthesis to denote how many meson it contains, $\left\lvert \psi \right\rangle^{(m)}$ indicates $\left\lvert \psi \right\rangle$ contains $m$ mesons, hence belongs to the $m$-meson Fock (sub)space. The superscript is sometimes inside the ket notation, sometimes out (as in here), I will in general not pay too much attention to it as long as it is clear what is meant;
- For an operator, we use the same notation to denote how many mesons it creates when acting on a state, for example $\mathcal{O}^{(m)}$ means that $\mathcal{O}^{(m)}\left\lvert \psi(n) \right\rangle$ as a whole has $m+n$ states.
There exists a nice diagrammatic symbol that Jarah created (Jarah diagram) to indicate different contributions. An explanation of how such diagrams work is given in the figure below.
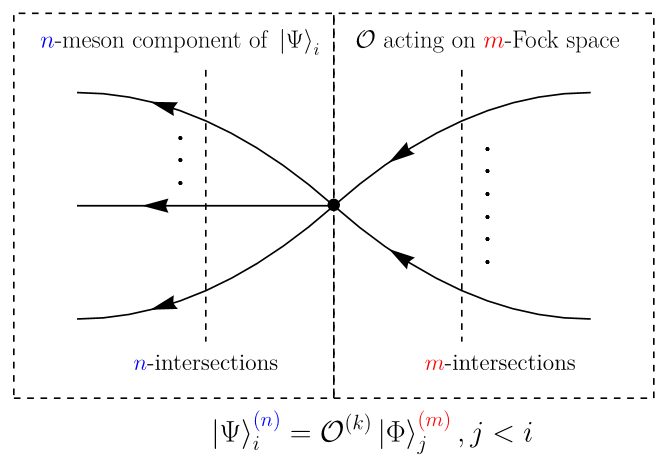
In the case of vacuum correction, I copy Jarah’s explanation here shamelessly.
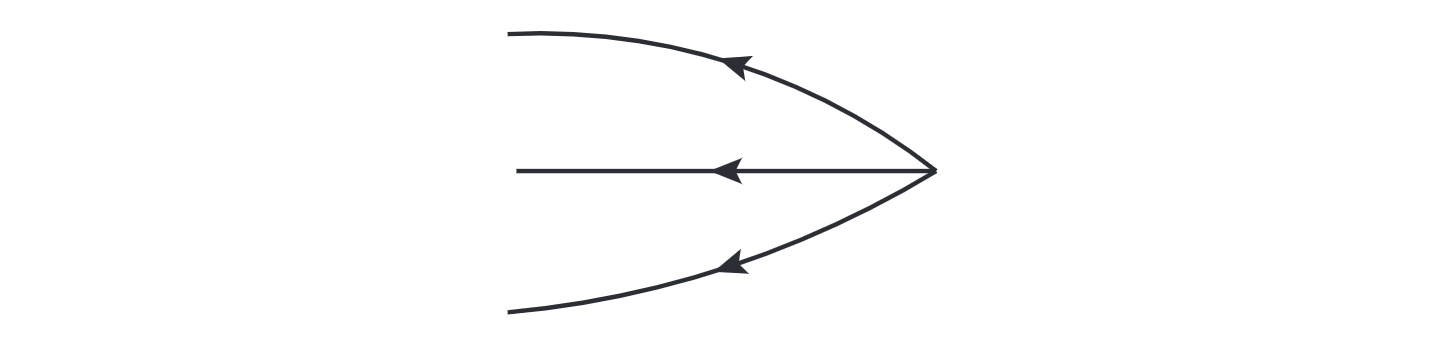
As an application of the notation we talked about, consider $H_ {3}$. It has different parts creating different numbers of operators, we write them as
\[H_ {3}= H_ {3}^{(-3)} + H_ {3}^{(-1)}+H_ {3}^{(1)}+H_ {3}^{(3)},\]where $H^{(-3)}$ is the part with three annihilation operators hence decrease the number of mesons by 3, etc. All these are summarized in the last chapter.
Now we can make use of the second HRC that defines the momenta eigenstates. It says
\[H _ {\text{full}} \left\lvert \vec{p} \right\rangle = \omega_ {p} \left\lvert \vec{p} \right\rangle ,\]we do the following expansion:
\[H_ {\text{full}} = \sum_ {i\geq 2} H_ {i} , \quad \left\lvert \vec{p} \right\rangle = \left\lvert \vec{p} \right\rangle_ {0}+\sum_ {j\geq 1} \left\lvert \vec{p} \right\rangle_ {1}^{(j)}\]since $H_ {2}\left\lvert \vec{p} \right\rangle_ {0}=\omega_ {0}\left\lvert \vec{p} \right\rangle_ {0}$, after some rearrangement we have the master formula
\[\boxed{ \sum_ {i\geq 3} H_ {i} \left\lvert \vec{p} \right\rangle_ {0}^{(1)} = \left( \omega_ {p}-\sum_ {i\geq 2}H_ {i} \right)\sum_ {j\geq 1} \left\lvert \vec{p} \right\rangle_ {1}^{(j)}. }\]Now, both parts will have contribution from different Fock space, for example $H_ {4}$ acting on $\left\lvert \vec{p} \right\rangle_ {0}^{(1)}$ may yield something with $2,3,\cdots$ free mesons. Now, besides matching the orders in coupling, we will also match the number of mesons.
Let’s see what happens at leading order $\sim g$ of the coupling. At this order, with regards to the Hamiltonian, we only need up to $H_ {3}$, thus the master formula reads
\[H_ {3}\left\lvert \vec{p} \right\rangle_ {0}^{(1)} = (\omega _ {p} -H_ {2}) \left\lvert \vec{p} \right\rangle_ {1}.\]There is not $H_ {3}\left\lvert \vec{p} \right\rangle_ {1}$ since $\left\lvert \vec{p} \right\rangle_ {1}\sim g$. Out goal is to express $\left\lvert \vec{p} \right\rangle_ {1}$ in terms of $\left\lvert \vec{p} \right\rangle_ {0}$.
The RHS adopts an expansion in Fock space:
\[(\omega_ {p}-H_ {2})\sum_ {n\geq 1}\left\lvert \vec{p} \right\rangle_ {1}^{(n)},\quad \text{with n mesons.}\]The same expansion on the left hand side reads
\[H_ {3} \left\lvert \vec{p} \right\rangle_ {0}^{(1)} = H_ {3}^{(-3)} \left\lvert \vec{p} \right\rangle_ {0}^{(1)} + H_ {3}^{(-1)} \left\lvert \vec{p} \right\rangle_ {0}^{(1)} + H_ {3}^{(1)} \left\lvert \vec{p} \right\rangle_ {0}^{(1)} + H_ {3}^{(3)} \left\lvert \vec{p} \right\rangle_ {0}^{(1)} ,\]Again, there is nothing else since $H_ {4}$ is of order $g^{2}$ already. To see how many particles (we will use particle and meson interchangeably in this note) are there, we just add all the upstairs number together, for example $H^{(3)}\left\lvert \vec{p} \right\rangle^{(1)}$ has $3+1=4$ particles in it.
Putting The LHS and RHS together we have
\[\sum_ {i}H_ {3}^{(i)} \left\lvert \vec{p} \right\rangle_ {0}^{(1)} = (\omega_ {p}-H_ {2})\sum_ {n\geq 1}\left\lvert \vec{p} \right\rangle_ {1}^{(n)}, \quad i\in \left\lbrace -3,-1,1,3 \,\middle\vert\, \right\rbrace .\]Balancing the superscripts, namely require $i+1=n$, we get
\[\begin{align*} H_ {3}^{(1)}\left\lvert \vec{p} \right\rangle_ {0}^{(1)} =& (\omega _ {p} -H_ {2}) \left\lvert \vec{p} \right\rangle_ {1}^{(2)}, \\ H_ {3}^{(3)}\left\lvert \vec{p} \right\rangle_ {0}^{(1)} =& (\omega _ {p} -H_ {2}) \left\lvert \vec{p} \right\rangle_ {1}^{(4)}. \end{align*}\]Next we need to substitute the expression for $H_ {3}$ in terms of ladder operator and contract, which can be found in the last section of the note. By the end of the day we get two components of $\left\lvert \vec{p} \right\rangle_ {1}$, namely the 2-free-meson and 4-free-meson components, as shown below:
\[\begin{align*} \left\lvert \vec{p} \right\rangle_ {1}^{(2)} &= (\omega _ {p} -H_ {2})^{-1}H_ {3}^{(1)} \left\lvert \vec{p} \right\rangle_ {0}^{(1)}, \\ \left\lvert \vec{p} \right\rangle_ {1}^{(4)} &= (\omega _ {p} -H_ {2})^{-1} H_ {3}^{(3)} \left\lvert \vec{p} \right\rangle_ {0}^{(1)}. \end{align*}\]Substitute the expression for $H_ {3}$ in terms of ladder operators, after some simplification we get
\[\left\lvert \vec{p} \right\rangle_ {1}^{(2)} = \frac{3mg}{2\sqrt{2}\omega _ {p} }\int \frac{d^{3}p_ {1}}{(2\pi)^{3}}\, \frac{\left\lvert \vec{p}_ {1},\vec{p}- \vec{p}_ {1} \right\rangle^{(2)}_ {0}}{\omega_ {p_ {1}}+\omega_ {p-p_ {1}}-\omega_ {p}} .\]Let’s take a closer look at $\left\lvert \vec{p} \right\rangle_ {1}^{(2)}$. Since $\omega(p)$ is not a linear function in $p$, considering $\vec{p}_ {1}+\vec{p}_ {2}=\vec{p}$, we have $\omega(\vec{p}_ {1})+\omega (\vec{p_ {2}}) \neq \omega(\vec{p})$, thus the integrand does not go to zero, hence is free of singularities.
Another component is
\[\left\lvert \vec{p} \right\rangle_ {1}^{(4)} = \frac{mg}{\sqrt{2}} \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \frac{d^{3}p_ {2}}{(2\pi)^{3}} \, \frac{\left\lvert \vec{p},\vec{p}_ {1,2,-1-2} \right\rangle_ {0}^{(4)}}{\omega_ {p_ {1}}+\omega_ {p_ {2}}+\omega_ {p_ {1}+p_ {2}}}.\]Order $g^{2}$
The Hamiltonian is
\[H_ {4}=\int d^{3}x : \mathcal{H}_ {4}:\]where the Hamiltonian density reads (we have used the relation for $\delta v_ {1}$)
\[\mathcal{H}_ {4} = \frac{g^{2}}{4}\phi^{4} + \phi^{2}\left( - \frac{\delta m_ {1}^{2}}{2} \right) + \phi(m^{2}\delta v_ {2})+ \frac{m^{4}(\delta g)^{2}}{16g^{4}} - \frac{m^{2}\delta v_ {1}^{2}}{2} + A_ 4,\]Let’s rewrite it as
\[\mathcal{H}_ {4} = \frac{g^{2}}{4} \phi^{4} + C_ {2} \phi^{2} + C_ {1} \phi + C_ {0}.\]The vacuum renormalization condition at order $g^{2}$ reads
\[H_ {4}\left\lvert \Omega_ {0} \right\rangle+H_ {3}\left\lvert \Omega_ {1} \right\rangle+H_ {2}\left\lvert \Omega_ {2} \right\rangle=0.\]We need to decompose $H_ {4}$ into Fock subspace. We already know how to do that for $\phi^{3}$, we just need to workout $\phi^{4}$. The same calculation we did for $H_ {3}$ gets us
\[\begin{align*} :\phi^{4}: =& :\phi^{4}:^{(4)}+:\phi^{4}:^{(2)}+:\phi^{4}:^{(0)}+:\phi^{4}:^{(-2)}+:\phi^{4}:^{(-4)},\\ :\phi^{4}:^{(4)} =& \int \prod_ {i=1}^{4} \frac{d^{3}p_ {i}}{(2\pi)^{3}} \, e^{ -i\vec{x}\cdot \sum_ {i=1}^{4}\vec{p}_ {i} } A^{\ddagger}_ {p_ {1}}A^{\ddagger}_ {p_ {2}}A^{\ddagger}_ {p_ {3}}A^{\ddagger}_ {p_ {4}} ,\\ :\phi^{4}:^{(2)} =& 4\int \prod_ {i=1}^{4} \frac{d^{3}p_ {i}}{(2\pi)^{3}} \, e^{ -i\vec{x}\cdot \sum_ {i=1}^{4}\vec{p}_ {i} } A^{\ddagger}_ {p_ {1}}A^{\ddagger}_ {p_ {2}}A^{\ddagger}_ {p_ {3}} \frac{A_ {-p_ {4}}}{2\omega_ {p_ {4}}} ,\\ :\phi^{4}:^{(0)} =& 6\int \prod_ {i=1}^{4} \frac{d^{3}p_ {i}}{(2\pi)^{3}} \, e^{ -i\vec{x}\cdot \sum_ {i=1}^{4}\vec{p}_ {i} } A^{\ddagger}_ {p_ {1}} A^{\ddagger}_ {p_ {2}} \frac{A_ {-p_ {3}}}{2\omega_ {p_ {3}}}\frac{A_ {-p_ {4}}}{2\omega_ {p_ {4}}} ,\\ :\phi^{4}:^{(-2)} =& 4\int \prod_ {i=1}^{4} \frac{d^{3}p_ {i}}{(2\pi)^{3}} \, e^{ -i\vec{x}\cdot \sum_ {i=1}^{4}\vec{p}_ {i} } A^{\ddagger}_ {p_ {1}} \frac{A_ {-p_ {2}}}{2\omega_ {p_ {2}}}\frac{A_ {-p_ {3}}}{2\omega_ {p_ {3}}}\frac{A_ {-p_ {4}}}{2\omega_ {p_ {4}}} ,\\ :\phi^{4}:^{(-4)} =& \int \prod_ {i=1}^{4} \frac{d^{3}p_ {i}}{(2\pi)^{3}} \, e^{ -i\vec{x}\cdot \sum_ {i=1}^{4}\vec{p}_ {i} } \frac{A_ {-p_ {1}}}{2\omega_ {p_ {1}}}\frac{A_ {-p_ {2}}}{2\omega_ {p_ {2}}}\frac{A_ {-p_ {3}}}{2\omega_ {p_ {3}}}\frac{A_ {-p_ {4}}}{2\omega_ {p_ {4}}} . \end{align*}\]Vacuum states correction
Let’s look at the 1-meson subspace first. There is no such contribution from $H_ {3}$. What about from $H_ {4}$? For $H_ {4}\left\lvert \Omega_ {0} \right\rangle^{(0)}$ to have one meson, we need $H_ {4}^{(1)}$ to act on $\left\lvert \Omega_ {0} \right\rangle$. We have
\(\begin{align*} \left\lvert \Omega_ {2} \right\rangle^{(1)} &= - H_ {2}^{-1} H_ {4}^{(1)} \left\lvert \Omega_ {0} \right\rangle, \\ &= - C_ {1} H_ {2}^{-1} :\phi:\left\lvert \Omega_ {0} \right\rangle \\ &= - \frac{C_ {1}}{m} \left\lvert \vec{p} \right\rangle_ {0}, \quad \vec{p}=0. \end{align*}\) The last condition, $p=0$, is required by momentum conservation.
The no-tadpole rule at order $g^{2}$ gives as that
\[\text{no-tadpole at }g^{2}: - \frac{C_ {1}}{m^{2}}+ \left\langle \Omega_ {1} \right\rvert\phi \left\lvert \Omega_ {1} \right\rangle=0,\]however $\left\lvert \Omega_ {1} \right\rangle$ has only 3-meson component, thus the second term in the above equation is zero, we have $C_ {1}=0$. This fixes another counter term:
\[\boxed{ \delta v_ {2}=0. }\]It simplifies the Hamiltonian to
\[\mathcal{H}_ {4}=\frac{g^{2}}{4} \phi^{4} - \frac{\delta m_ {1}^{2}}{2} \phi^{2} + C_ {0}.\]In general the no-tadpole rule require the linear term in $\phi$ to vanish, and the true-vacuum condition require the constant term to vanish, which we will check later.
Introduce the shorthand notation $\left\lvert \vec{p}_ {-1-2} \right\rangle:=\left\lvert -\vec{p}_ {1}-\vec{p}_ {2} \right\rangle$, $\left\lvert \vec{p}_ {-1’-2’} \right\rangle:=\left\lvert -\vec{p}’_ {1}-\vec{p}’_ {2} \right\rangle$ and $\left\lvert \vec{p}_ {1,2} \right\rangle:=\left\lvert \vec{p}_ {1}\vec{p}_ {2} \right\rangle$. Also let’s write $\omega_ {1}=\omega_ {p_ {1}},\, \omega_ {1’}=\omega_ {\vec{p}_ {1}’},\,\omega_ {1+2}=\omega_ {p_ {1}+p_ {2}}$ and
\[\frac{d^{3}p_ {1,2,1',2'}}{(2\pi)^{12}} := \frac{d^{3}p_ {1}}{(2\pi)^{3}}\frac{d^{3}p_ {2}}{(2\pi)^{3}}\frac{d^{3}p'_ {1}}{(2\pi)^{3}}\frac{d^{3}p'_ {2}}{(2\pi)^{3}}.\]The decomposition of $H_ {4}$ by meson numbers reads
\[\begin{align*} H_ {4} =& \sum_ {n=0}^{4} H_ {4}(4-2n), \\ H_ {4}^{(4)} =& \frac{g^{2}}{4} \int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}} \, A^{\ddagger}_ {1}A^{\ddagger}_ {2}A^{\ddagger}_ {3}A^{\ddagger}_ {-1-2-3} ,\\ H_ {4}^{(2)} =& g^{2} \int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}} \, A^{\ddagger}_ {1}A^{\ddagger}_ {2}A^{\ddagger}_ {3} \frac{A_ {1+2+3}}{2\omega_ {1+2+3}} \\ &- \frac{\delta m_ {1}^{2}}{2} \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, A_ {1}^{\ddagger}A_ {-1}^{\ddagger},\\ H_ {4}^{(0)} =& \frac{3g^{2}}{2} \int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}}\, A^{\ddagger}_ {1} A^{\ddagger}_ {2} \frac{A_ {-3}}{2\omega_ {3}}\frac{A_ {1+2+3}}{2\omega_ {1+2+3}} \\ &- \delta m_ {1}^{2} \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \frac{A_ {1}^{\ddagger}A_ {1}}{2\omega_ {1}}+\int d^{3}x \, C_ {0} ,\\ H_ {4}^{(-2)} =& g^{2}\int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}}\, A^{\ddagger}_ {1} \frac{A_ {-2}}{2\omega_ {2}}\frac{A_ {-3}}{2\omega_ {3}}\frac{A_ {1+2+3}}{2\omega_ {1+2+3}} \\ & -\frac{\delta m_ {1}^{2}}{2}\int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \frac{A_ {1}A_ {-1}}{(2\omega_ {1})^{2}} , \\ H_ {4}^{(-4)} =& \frac{g^{2}}{4} \int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}}\, \frac{A_ {-1}}{2\omega_ {1}}\frac{A_ {-2}}{2\omega_ {2}}\frac{A_ {-3}}{2\omega_ {3}}\frac{A_ {1+2+3}}{2\omega_ {1+2+3}} , \end{align*}\]where we have used the condition that $\vec{p}_ {1}+\vec{p}_ {2}+\vec{p}_ {3}+\vec{p}_ {4}=0$.
We have now all the ingredients needed to solve
\[\boxed{ \left\lvert \Omega_ {2} \right\rangle=-H_ {2}^{-1} H_ {4}\left\lvert \Omega_ {0} \right\rangle - H_ {2}^{-1} H_ {3}\left\lvert \Omega_ {1} \right\rangle, }\]one meson number at a time. We will go from $6$ mesons and down to $0$ mesons.
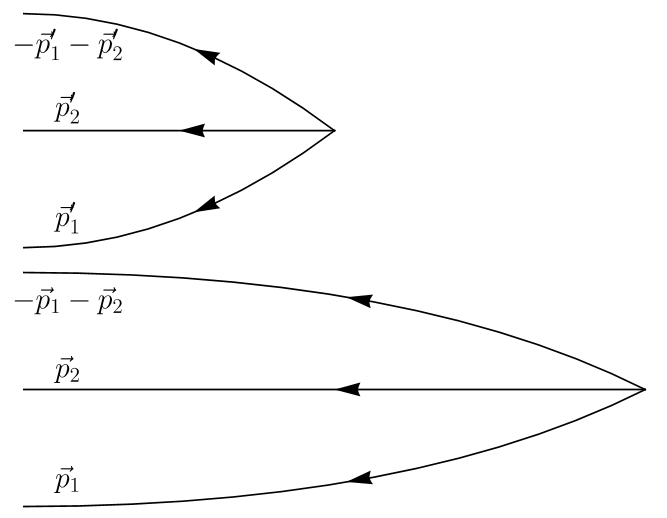
In $6$-meson Fock space we have
\[\begin{align*} \left\lvert \Omega_ {2} \right\rangle^{(6)} =& -H_ {2}^{-1} H_ {3}^{(3)}\left\lvert \Omega_ {1} \right\rangle^{(3)} \\ =&\frac{m^{2}g^{2}}{2} \int \frac{d^{3}p_ {1,2,1',2'}}{(2\pi)^{12}} \, \\ &\times \frac{\left\lvert \vec{p}_ {1,2,-1-2}\;\vec{p}'_ {1,2,-1-2} \right\rangle_ {0}}{(\omega_ {1}+\omega_ {2}+\omega_ {1+2})(\omega_ {1}+\omega_ {2}+\omega_ {1+2}+\omega_ {1}'+\omega_ {2}'+\omega_ {1'+2'})} \end{align*}\]where
\[\left\lvert \vec{p}'_ {1,2,-1-2} \right\rangle_ {0} := \left\lvert \vec{p}'_ {1},\vec{p}'_ {2},\vec{p}'_ {-1-2} \right\rangle_ {0} := \left\lvert \vec{p}'_ {1},\vec{p}'_ {2},-\vec{p}'_ {1}-\vec{p}'_ {2} \right\rangle_ {0}.\]This is represented by the figure below. Note the manifestation of momentum conservation.
In the case of 4-mesons, both $H_ {3}$ and $H_ {4}$ contribute. The contribution from $H_ {4}$ is simpler:
\[- H_ {2}^{-1} H_ {4}\left\lvert \Omega_ {0} \right\rangle= - \frac{g^{2}}{4} \int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}} \, \frac{\left\lvert \vec{p}_ {1,2,3,-1-2-3} \right\rangle_ {0}}{\omega_ {1}+\omega_ {2}+\omega_ {3}+\omega_ {1+2+3}} ,\]while the contribution from $H_ {3}\left\lvert \Omega_ {1} \right\rangle$ is more complicated due to the expansion of $\left\lvert \Omega_ {1} \right\rangle$, we have
\[\begin{align*} H_ {3}^{(1)}\left\lvert \Omega_ {1} \right\rangle^{(3)} =& -\frac{mg}{\sqrt{2}} \int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}}\, \frac{3}{2\omega_ {1+2}}A_ {1}^{\ddagger}A_ {2}^{\ddagger}A_ {1+2} \times \frac{mg}{\sqrt{2}} \int \frac{d^{3}p_ {1',2'}}{(2\pi)^{6}} \, \frac{\left\lvert \vec{p}_ {1',2',-1'-2'}\right\rangle_ {0} }{(\omega_ {1'}+\omega_ {2'}+\omega_ {3'})}\\ =& - \frac{m^{2}g^{2}}{2}\int \frac{d^{3}p_ {1,2,1',2'}}{(2\pi)^{12}} \, \frac{3A_ {1}^{\ddagger}A_ {2}^{\ddagger}A_ {1+2}A_ {1'}^{\ddagger}A^{\ddagger}_ {2'}A^{\ddagger}_ {-1'-2'}\left\lvert \Omega_ {0} \right\rangle}{2\omega_ {1+2}(\omega_ {1'}+\omega_ {2'}+\omega_ {3'})}\\ =& - \frac{9m^{2}g^{2}}{4}\int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}} \, \frac{\left\lvert \vec{p}_ {1,2,3,-1-2-3} \right\rangle_ {0}}{\omega_ {1+2}(\omega_ {1+2}+\omega_ {3}+\omega_ {1+2+3})} \end{align*}\]where all the contractions offer a factor of 3 and $\left\lvert \vec{p}_ {1,2,3,-1-2-3} \right\rangle$ is a short-handed notation for $\left\lvert \vec{p}_ {1} \vec{p}_ {2} \vec{p}_ {3},-\vec{p}_ {1} -\vec{p}_ {2} -\vec{p}_ {3}\right\rangle$.
Thus
\[\begin{align*} -H_ {2}^{-1} H_ {3}\left\lvert \Omega_ {1} \right\rangle =& \left( \frac{3mg}{2} \right)^{2} \int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}} \, \frac{1}{\omega_ {1+2}(\omega_ {1+2}+\omega_ {3}+\omega_ {1+2+3})} \\ &\times \frac{\left\lvert \vec{p}_ {1,2,3,-1-2-3} \right\rangle_ {0}}{(\omega_ {1}+\omega_ {2}+\omega_ {3}+\omega_ {1+2+3})}. \end{align*}\]Putting them together we have
\[\boxed{ \begin{align*} \left\lvert \Omega_ {2} \right\rangle^{(4)} = & \frac{g^{2}}{4} \int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}} \, \left( \frac{9m^{2}}{\omega_ {1+2}(\omega_ {1+2}+\omega_ {3}+\omega_ {1+2+3})} -1\right) \\ &\times \frac{\left\lvert \vec{p}_ {1,2,3,-1-2-3} \right\rangle_ {0}}{\omega_ {1}+\omega_ {2}+\omega_ {3}+\omega_ {1+2+3}} \end{align*} }\]We move on to calculate $\left\lvert \Omega_ {2} \right\rangle^{(2)}=-H_ {2}^{-1} H_ {4}^{(2)}\left\lvert \Omega_ {0} \right\rangle - H_ {2}^{-1} H_ {3}^{(-1)}\left\lvert \Omega_ {1}\right\rangle^{(3)}$. We get
\[\begin{align*} - \frac{1}{H_ {2}}H_ {4}^{(2)}\left\lvert \Omega_ {0} \right\rangle =& \frac{1}{2}\delta m^{2} \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \frac{\left\lvert \vec{p}_ {1,-1} \right\rangle_ {0}}{2\omega_ {1}} \\ - \frac{1}{H_ {2}}H_ {3}^{(-1)}\left\lvert \Omega_ {1}\right\rangle^{(3)} =& \frac{9m^{2}g^{2}}{4} \int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}} \, \frac{\left\lvert \vec{p}_ {1,-1} \right\rangle_ {0}}{\omega_ {2}\omega_ {1+2}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})2\omega_ {1}}. \end{align*}\]Putting them together we get
\[\left\lvert \Omega \right\rangle^{(2)}_ {2}=\int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \left\lbrace \delta m^{2}+\frac{9 m^{2}g^{2}}{2} \int \frac{d^{3}p_ {2}}{(2\pi)^{3}} \, \frac{1}{\omega_ {2}\omega_ {1+2}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})} \right\rbrace \frac{\left\lvert \vec{p}_ {1,-1} \right\rangle_ {0}}{4\omega_ {1}} .\]The integral over $p_ {2}$ has superfacial degree of divergent $3-3=0$, thus adopts logarithmic divergence. This divergence ought to be canceled by $\delta m^{2}$, as we will check later. If that’s true then $\left\lvert \Omega \right\rangle^{(2)}_ {2}=0.$
The HRC1 equation reads
\[H_ {4}^{0}\left\lvert \Omega_ {0} \right\rangle+H_ {3}^{(-3)}\left\lvert \Omega_ {1}^{(3)} \right\rangle+H_ {2}\left\lvert \Omega_ {2} \right\rangle^{(0)}=0,\]but $\left\lvert \Omega_ {2} \right\rangle^{(0)}$ does not exist by construction, if $\left\lvert \Omega_ {2} \right\rangle$ has any $\left\lvert \Omega_ {0} \right\rangle$ component we can absorbe it into the $\left\lvert \Omega_ {0} \right\rangle$ itself. So we are left with
\[H_ {4}^{(0)}\left\lvert \Omega_ {0} \right\rangle+H_ {3}^{(-3)}\left\lvert \Omega_ {1}^{(3)} \right\rangle=0,\]This fixes the counter terms. The contribution from $H_ {4}^{(0)}$ is a divergent constant:
\[H_ {4}^{(0)}\left\lvert \Omega_ {0} \right\rangle = \int d^{3}x \, C_ {0} \left\lvert \Omega_ {0} \right\rangle.\]So the contribution from $H_ {3}$ must cancel it. In order to compare the above result, we need to keep the $\int d^{3}x$ integral, writing $H_ {3}^{(-3)}$ as
\[H_ {3}^{(-3)} = -\frac{mg}{\sqrt{2}} \int d^{3}x \, e^{ -i\vec{x}\cdot(\vec{p}_ {1}+\vec{p}_ {2}+\vec{p}_ {3}) } \int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}}\, \frac{1}{2\omega_ {1}2\omega_ {2}2\omega_ {3}} A_ {-1}A_ {-2}A_ {-3} .\]Similar to the calculation before, we have
\[\begin{align*} H_ {3}^{(-3)} \left\lvert \Omega_ {1} \right\rangle^{3} =& -\frac{mg}{\sqrt{2}} \int d^{3}x \int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}}\, \frac{1}{2\omega_ {1}2\omega_ {2}2\omega_ {3}} A_ {-1}A_ {-2}A_ {-3}\\ &\times \frac{mg}{\sqrt{2}} \int \frac{d^{3}p_ {1}'}{(2\pi)^{3}} \frac{d^{3}p_ {2}'}{(2\pi)^{3}} \, \frac{\left\lvert \vec{p}_ {1}'\vec{p}_ {2}',-\vec{p}_ {1}'-p_ {2}' \right\rangle_ {0} }{(\omega_ {p_ {1}'}+\omega_ {p_ {2}'}+\omega_ {p_ {1}'+p_ {2}'})}\\ =& -\frac{3g^{2}m^{2}}{8} \int d^{3}x \int \frac{d^{3}p_ {1}d^{3}p_ {2}}{(2\pi)^{6}} \, \frac{\left\lvert \Omega \right\rangle_ {0}}{\omega_ {p_ {1}}\omega_ {p_ {2}}\omega_ {p_ {1}+p_ {2}}(\omega_ {p_ {1}}+\omega_ {p_ {2}}+\omega_ {p_ {1}+p_ {2}})} . \end{align*}\]To cancel the divergence, we obviously need
\[C_ {0} = A_ {4}' \equiv \frac{3g^{2}m^{2}}{8} \int \frac{d^{3}p_ {1}d^{3}p_ {2}}{(2\pi)^{6}} \, \frac{1}{\omega_ {p_ {1}}\omega_ {p_ {2}}\omega_ {p_ {1}+p_ {2}}(\omega_ {p_ {1}}+\omega_ {p_ {2}}+\omega_ {p_ {1}+p_ {2}})} .\]Momentum states corrections
Next we turn to the renormalization condition for the momentum eigenstates. At order $g^{2}$ this conditions reads
\[(\omega_ {p}-H_ {2})\left\lvert p \right\rangle_ {2} = H_ {4} \left\lvert \vec{p} \right\rangle_ {0} +H_ {3}\left\lvert p \right\rangle_ {1} .\]Again we start from the highest meson number and go downwards. The highest possible particle number comes from $H_ {3}^{(3)}\left\lvert \vec{p} \right\rangle_ {1}^{(4)}$, which is simple since there only exists creation operators. It reads:
\[\left\lvert \vec{p} \right\rangle_ {2}^{(7)} = \frac{m^{2}g^{2}}{2} \int \frac{d^{3}p_ {1,2,3,4}}{(2\pi)^{12}} \, \frac{\left\lvert \vec{p},\vec{p}_ {1,2,3,4,-1-2,-3-4} \right\rangle_ {0}}{(\omega_ {1}+\omega_ {2}+\omega_ {1+2})(\omega_ {1}+\omega_ {2}+\omega_ {3}+\omega_ {4}+\omega_ {1+2}+\omega_ {3+4})}.\]Next Fock space is $5$, coming from the following contributions:
\[H_ {4}^{(4)} \left\lvert \vec{p} \right\rangle_ {0}^{(1)} = \frac{g^{2}}{4} \int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}} \, \left\lvert \vec{p},\vec{p}_ {1,2,3,-1-2-3} \right\rangle_ {0} ,\] \[H_ {3}^{(3)} \left\lvert \vec{p} \right\rangle_ {1}^{(2)} = \frac{3g^{2}m^{2}}{4\omega_ {p}}\int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}} \, \frac{\left\lvert \vec{p}-\vec{p}_ {1}, \vec{p}_ {1,2,3,-2-3} \right\rangle_ {0}}{\omega _ {p}-\omega_ {1}-\omega_ {p-p_ {1}}}\]and
\[H_ {3}^{(1)} \left\lvert \vec{p} \right\rangle_ {1}^{(4)} = - \frac{3g^{2}m^{2}}{4} \int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}} \, \left( \frac{3\left\lvert \vec{p},\vec{p}_ {1,2,3,-1-2-3} \right\rangle_ {0}}{\omega_ {2+3}(\omega_ {1}+\omega_ {2+3}+\omega_ {1+2+3})} + \frac{\left\lvert \vec{p}_ {1,2,3,-1-2},\vec{p}-\vec{p}_ {3} \right\rangle_ {0}}{\omega_ {p}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})} \right)\]Does the first term agrees with Jarah’s result? The second term is fine as it is.
Altogether these lead to
\[\begin{align*} \left\lvert \vec{p}\right\rangle_ {2}^{(5)} =& \frac{g^{2}}{4}\int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}} \, \left( \frac{9m^{2}}{\omega_ {2+3}(\omega_ {1}+\omega_ {2+3}+\omega_ {1+2+3})}-1 \right) \frac{\left\lvert \vec{p},\vec{p}_ {1,2,3,-1-2-3} \right\rangle_ {0}}{\omega_ {1}+\omega_ {2}+\omega_ {3}+\omega_ {1+2+3}} \\ &+ \frac{3g^{2}m^{2}}{4\omega _ {p} }\int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}} \, \frac{\left\lvert \vec{p}_ {1,2,3,-1-2},\vec{p}-\vec{p}_ {3} \right\rangle_ {0}}{(\omega_ {1}+\omega_ {2}+\omega_ {1+2})(\omega_ {3}+\omega_ {p+p_ {3}}-\omega_ {p})}. \end{align*}\]3-Fock space comes from
\[(\omega_ {p}-H_ {2})\left\lvert \vec{p} \right\rangle_ {2}^{(3)} = H_ {4}^{(2)} \left\lvert \vec{p} \right\rangle_ {0}^{(1)} +H_ {3}^{(1)}\left\lvert \vec{p} \right\rangle_ {1}^{(2)} +H_ {3}^{(-1)}\left\lvert \vec{p} \right\rangle_ {1}^{(4)}.\]Same as before, we get:
\[\begin{align*} H_ {4}^{(2)} \left\lvert \vec{p} \right\rangle_ {0}^{(1)} =& \frac{g^{2}}{2\omega_ {p}} \int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}}\left\lvert \vec{p}-\vec{p}_ {1}-\vec{p}_ {2},\vec{p}_ {1,2} \right\rangle_ {0} -\frac{\delta m^{2}}{2}\int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \left\lvert \vec{p},\vec{p}_ {1,-1} \right\rangle_ {0}, \\ H_ {3}^{(1)}\left\lvert \vec{p} \right\rangle_ {1}^{(2)} =& - \frac{9g^{2}m^{2}}{4\omega_ {p}} \int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}} \, \frac{\left\lvert \vec{p}-\vec{p}_ {1}-\vec{p}_ {2},\vec{p}_ {1,2} \right\rangle_ {0}}{\omega_ {1+2}(-\omega _ {p} +\omega_ {p-p_ {1}-p_ {2}}+\omega_ {1+2})} ,\\ H_ {3}^{(-1)}\left\lvert \vec{p} \right\rangle_ {1}^{(4)} =& - \frac{9m^{2}g^{2}}{4} \int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}} \, \frac{\left\lvert \vec{p},\vec{p}_ {1,-1} \right\rangle_ {0}}{\omega_ {2}\omega_ {1+2}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})}\\ &- \frac{9m^{2}g^{2}}{4\omega _ {p} } \int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}} \, \frac{\left\lvert \vec{p}-\vec{p}_ {1}-\vec{p}_ {2},\vec{p}_ {1,2} \right\rangle_ {0}}{\omega_ {1+2}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})} \end{align*}\]Inverting $\omega _ {p}-H_ {2}$ we get
\[\begin{align*} \left\lvert \vec{p} \right\rangle_ {2}^{(3)} =& \frac{g^{2}}{4\omega _ {p} }\int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}} \, \left( -2+\frac{9m^{2}}{\omega_ {1+2}}\left( \frac{1}{-\omega _ {p} +\omega_ {p-p_ {1}-p_ {2}}+\omega_ {1+2}} + \frac{1}{\omega_ {1}+\omega_ {2}+\omega_ {1+2}} \right) \right)\\ &\times \frac{\left\lvert \vec{p}_ {1,2},\vec{p}-\vec{p}_ {1}-\vec{p}_ {2} \right\rangle_ {0}}{-\omega _ {p} +\omega_ {1}+\omega_ {2}+\omega_ {p-p_ {1}-p_ {2}}} \\ &- \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \left( \delta m^{2} + \frac{9m^{2}g^{2}}{2}\int \frac{d^{3}p_ {2}}{(2\pi)^{3}} \, \frac{1}{\omega_ {2}\omega_ {1+2}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})} \right) \frac{\left\lvert \vec{p},\vec{p}_ {1,-1} \right\rangle_ {0}}{4\omega_ {1}}. \end{align*}\]As a consistancy check, this renormalization condition for $\delta m^{2}$ is the same as that we got from $\left\lvert \Omega_ {2} \right\rangle$.
1-Fock space comes from
We have
\[(\omega_ {p}-H_ {2})\left\lvert \vec{p} \right\rangle_ {2}^{(1)} = H_ {4}^{(0)} \left\lvert \vec{p} \right\rangle_ {0}^{(1)} +H_ {3}^{(-1)}\left\lvert \vec{p} \right\rangle_ {1}^{(2)} +H_ {3}^{(-3)}\left\lvert \vec{p} \right\rangle_ {1}^{(4)}.\]During the computation sometimes we need again to keep $d^{3}x$ when dealing with conter terms.
we have
\[\begin{align*} H_ {4}^{(0)}\left\lvert p \right\rangle_ {0}^{(1)} =& A_ {4}'\int d^{3}x \, \left\lvert \vec{p} \right\rangle_ {0} - \frac{\delta m^{2}}{2\omega _ {p} }\left\lvert \vec{p} \right\rangle_ {0},\\ H_ {3}^{(-1)}\left\lvert \vec{p} \right\rangle_ {1}^{(2)} =& -\frac{9g^{2}m^{2}}{8\omega _ {p} } \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \frac{\left\lvert \vec{p} \right\rangle_ {0}}{\omega_ {1}\omega_ {p+p_ {1}}(-\omega _ {p} +\omega_ {1}+\omega_ {p+p_ {1}})},\\ H_ {3}^{(-3)}\left\lvert p \right\rangle_ {1}^{(4)} =& - \frac{9g^{2}m^{2}\left\lvert \vec{p} \right\rangle_ {0}}{8\omega _ {p} }\int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \frac{1}{\omega_ {1}\omega_ {p+p_ {1}}(\omega _ {p} +\omega_ {1}+\omega_ {p+p_ {1}})}\\ &- \frac{3}{8}g^{2}m^{2}\delta^{3}(0) \left\lvert \vec{p} \right\rangle_ {0} \int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}} \, \frac{1}{\omega_ {1}\omega_ {2}\omega_ {1+2}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})}. \end{align*}\]In the last term if we write $(2\pi)^{3}\delta^{3}(0)=\int d^{3}x$ then it cancels with the $A_ {4}’$ term.
Another approach is to use
\[\int d^{3}x \, \left( - \frac{\delta m^{2}}{2} :\phi^{2}: \right) = - \frac{\delta m^{2}}{2}\int d^{3}x \frac{d^{3}p_ {1,2}}{(2\pi)^{6}} \, e^{ -i\vec{x}\cdot(\vec{p}_ {1}+\vec{p}_ {2}) } \left( A^{\ddagger}_ {1,2}+2A^{\ddagger}_ {1} \frac{A_ {-2}}{2\omega_ {1}}+\frac{A_ {-1,-2}}{2\omega_ {1}2\omega_ {2}} \right).\]Now recall that due to the conservation of momentum, $(\omega_ {p}-H_ {2})\left\lvert \vec{p} \right\rangle_ {2}^{(1)} =0$, this allows as to calculate $\delta m^{2}$,
\[\begin{align*} \frac{\delta m^{2}}{2\omega _ {p} } =&- \frac{9m^{2}g^{2}}{8\omega _ {p} }\int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \frac{1}{\omega_ {1}\omega_ {p+p_ {1}}(-\omega _ {p} +\omega_ {1}+\omega_ {p+p_ {1}})} \\ &- \frac{9g^{2}m^{2}}{8\omega _ {p} } \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \frac{1}{\omega_ {1}\omega_ {p+ {p_ {1}}}(\omega _ {p} +\omega_ {1}+\omega_ {p+p_ {1}})} \\ =& - \frac{9m^{2}g^{2}}{8\omega _ {p} }\int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \frac{1}{\omega_ {1}\omega_ {p+p_ {1}}} \left( \frac{2(\omega_ {1}+\omega_ {p+p_ {1}})}{(\omega_ {1}+\omega_ {p+p_ {1}})^{2}-\omega p^{2}} \right)\\ \approx &- \frac{9g^{2}m^{2}}{16\pi^{2}\omega _ {p} }\ln\left( \frac{\Lambda}{m} \right) + \text{const},\\ \implies \delta m^{2} =& - \frac{9g^{2}m^{2}}{8\pi^{2}}\ln\left( \frac{\Lambda}{m} \right) + \text{const} \end{align*}\]The constant part can be fixed later.
As for the orthogonal condition, we can check that $_ {0}\left\langle \vec{p}_ {1,2} \middle\vert \vec{p}\right\rangle_ {2}$ indeed is zero.
Coupling counter term at order $g^{3}$
The 3rd-order Hamiltonian density reads
\[\mathcal{H}_ {5} = C_ {3}\phi^{3}+ C_ {1}\phi + C_ {0}.\]where
\[\begin{align*} C_ {3}=& \frac{m\delta g}{\sqrt{2}} +\frac{g \delta m_ {1}^{2}}{2\sqrt{2}m} - \frac{m^{2}\delta m_ {1}^{4}}{2\sqrt{2}g}, \\ C_ {1}=& m^{2}\delta v_ {3}-\frac{3gm\mathcal{I}_ {1}}{\sqrt{2}}+\frac{m^{3}\delta g^{2}}{\sqrt{2}g^{3}}-\frac{m \delta g\delta m_ {1}^{2}}{2\sqrt{2}g^{2}} -\frac{\delta m_ {1}^{4}}{8\sqrt{2}gm},\\ C_ {0}=& A_ {5}. \end{align*}\]We have the renormalization condition saying that the interaction vacuum is really a vacuum, $H\left\lvert \Omega \right\rangle=0$, the $\left\lvert \Omega_ {0} \right\rangle$ component of it then requires that $C_ {0}=A_ {5}=0$.
Since we have
\[\begin{align*} \int d^{3}x : \phi^{3}:^{(3)} =& \int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}}\, A_ {1}^{\ddagger}A_ {2}^{\ddagger}A_ {-1-2}^{\ddagger} \\ \int d^{3}x:\phi^{3}:^{(1)} =& \int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}}\, \frac{3}{2\omega_ {1+2}}A_ {1}^{\ddagger}A_ {2}^{\ddagger}A_ {1+2}\\ \int d^{3}x:\phi^{3}:^{(-1)} =& \int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}}\,\frac{3}{2\omega_ {2}} \frac{1}{2\omega_ {1+2}} A_ {1}^{\ddagger}A_ {-2} A_ {1+2} \\ \int d^{3}x:\phi^{3}:^{(-3)} =& \int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}}\, \frac{1}{2\omega_ {1}2\omega_ {2}2\omega_ {1+2}} A_ {-1}A_ {-2}A_ {1+2} \end{align*}\]we have
\[\begin{align*} H_ {5}=& H_ {5}^{(3)}+H_ {5}^{(1)}+H_ {5}^{(-1)}+H_ {5}^{(-3)} ,\\ H_ {5}^{(3)}=& C_ {3}\int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}}\, A_ {1}^{\ddagger}A_ {2}^{\ddagger}A_ {-1-2}^{\ddagger} ,\\ H_ {5}^{(1)}=& C_ {3}\int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}}\, \frac{3}{2\omega_ {1+2}}A_ {1}^{\ddagger}A_ {2}^{\ddagger}A_ {1+2} +C_ {1}A_ {0}^{\ddagger} ,\\ H_ {5}^{(-1)}=&C_ {3} \int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}}\,\frac{3}{2\omega_ {2}} \frac{1}{2\omega_ {1+2}} A_ {1}^{\ddagger}A_ {-2} A_ {1+2} + C_ {1} \frac{A_ {0}}{2m} ,\\ H_ {5}^{(-3)}=& C_ {3}\int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}}\, \frac{1}{2\omega_ {1}2\omega_ {2}2\omega_ {1+2}} A_ {-1}A_ {-2}A_ {1+2} ,\\ \end{align*}\]The vacuum correction
where $C_ {3},C_ {1}$ are parameters to be determined. As before the equation for $\left\lvert \Omega \right\rangle_ {3}$ is :
\[\left\lvert \Omega \right\rangle_ {3} = -H_ {2}^{-1}(H_ {5}\left\lvert \Omega \right\rangle_ {0}+H_ {4}\left\lvert \Omega \right\rangle_ {1}+H_ {3}\left\lvert \Omega \right\rangle_ {2}),\]if separate into different Fock spaces we get
\[\begin{align*} - H_ {2}\left\lvert \Omega \right\rangle_ {3}^{(9)} =& H_ {3}^{(3)} \left\lvert \Omega \right\rangle_ {2}^{(6)},\\ - H_ {2}\left\lvert \Omega \right\rangle_ {3}^{(7)} =& H_ {3}^{(3)} \left\lvert \Omega \right\rangle_ {2}^{(4)}+H_ {3}^{(1)} \left\lvert \Omega \right\rangle_ {2}^{(6)}+H_ {4}^{(4)}\left\lvert \Omega \right\rangle_ {1}^{(3)},\\ - H_ {2}\left\lvert \Omega \right\rangle_ {3}^{(5)} =& H_ {3}^{(1)}\left\lvert \Omega \right\rangle_ {2}^{(4)} +H_ {3}^{(-1)}\left\lvert \Omega \right\rangle_ {2}^{(6)} +H_ {4}^{(2)}\left\lvert \Omega \right\rangle_ {1}^{(3)}, \\ - H_ {2}\left\lvert \Omega \right\rangle_ {3}^{(3)} =& H_ {3}^{(-1)}\left\lvert \Omega \right\rangle_ {2}^{(4)} +H_ {3}^{(-3)}\left\lvert \Omega \right\rangle_ {2}^{(6)} +H_ {4}^{(0)} \left\lvert \Omega \right\rangle_ {1}^{(3)}, \\ - H_ {2}\left\lvert \Omega \right\rangle_ {3}^{(1)} =& H_ {3}^{(-3)}\left\lvert \Omega \right\rangle_ {2}^{(4)}+H_ {4}^{(-2)}\left\lvert \Omega \right\rangle_ {1}^{(3)}+H_ {5}^{(1)}\left\lvert \Omega \right\rangle_ {0}. & \end{align*}\]Substitute the ingredients and simplify as before, we get the following results.
$\left\lvert \Omega \right\rangle_ {3}^{(9)}:$
\(\begin{align*} \left\lvert \Omega \right\rangle_ {3}^{(9)} =& \frac{g^{3}m^{3}}{2\sqrt{2}}\int \frac{d^{3}p_ {1,2,3,4,5,6}}{(2\pi)^{18}} \, \frac{1}{(\omega_ {1}+\omega_ {2}+\omega_ {1+2})(\omega_ {1}+\omega_ {2}+\omega_ {3}+\omega_ {4}+\omega_ {1+2}+\omega_ {3+4})} \\ &\times \frac{\left\lvert \vec{p}_ {1,2,3,4,5,6},-\vec{p}_ {1}-\vec{p}_ {2},-\vec{p}_ {3}-\vec{p}_ {4},-\vec{p}_ {5}-\vec{p}_ {6} \right\rangle_ {0}}{(\omega_ {1}+\omega_ {2}+\omega_ {3}+\omega_ {4}+\omega_ {5}+\omega_ {6}+\omega_ {1+2}+\omega_ {3+4}+\omega_ {5+6})} \end{align*}\)
$\left\lvert \Omega \right\rangle_ {3}^{(7)}:$
\[\begin{align*} H_ {3}^{(3)}\left\lvert \Omega \right\rangle_ {2}^{(4)} =& -\frac{g^{3}m}{4\sqrt{2}}\int \frac{d^{3}p_ {1,2,3,4,5}}{(2\pi)^{15}} \, \frac{ \frac{9m^{2}}{\omega_ {3+4}(\omega_ {3+4}+\omega_ {5}+\omega_ {3+4+5})}-1 }{\omega_ {3}+\omega_ {4}+\omega_ {5}+\omega_ {3+4+5}} \left\lvert \vec{p}_ {1,2,3,4,5},\vec{p}_ {-1-2},\vec{p}_ {-3-4-5} \right\rangle_ {0},\\ H_ {3}^{(1)}\left\lvert \Omega \right\rangle_ {2}^{(6)} =& -\frac{9 g^3 m^3}{4 \sqrt{2}} \int \frac{d^{3}p_ {1,2,3,4,5}}{(2\pi)^{15}} \, \frac{\left\lvert \vec{p}_ {1,2,3,4,5,-1-2-3,-4-5} \right\rangle_ {0}}{\omega_ {1+2}(\omega_ {1+2}+\omega_ {3}+\omega_ {1+2+3})(\omega_ {4}+\omega_ {5}+\omega_ {4+5})}, \\ H_ {4}^{(4)}\left\lvert \Omega \right\rangle_ {1}^{(3)} =& \frac{g^{3}m}{4\sqrt{2}} \int \frac{d^{3}p_ {1,2,3,4,5}}{(2\pi)^{15}} \, \frac{\left\lvert \vec{p}_ {1,2,3,4,5,-1-2-3,-4-5} \right\rangle_ {0}}{\omega_ {4}+\omega_ {5}+\omega_ {4+5}}. \end{align*}\]Put altogether and inverse $-H_ {2}$, we get:
\[\left\lvert \Omega \right\rangle_ {3}^{(7)} = \frac{g^{3}m}{4\sqrt{2}}\int \frac{d^{3}p_ {1,2,3,4,5}}{(2\pi)^{15}} \, \frac{\left( \frac{9m^{2}}{\omega_ {1+2}(\omega_ {1+2}+\omega_ {3}+\omega_ {1+2+3})}-1 \right)\left\lvert \vec{p}_ {1,2,3,4,5,-1-2-3,-4-5} \right\rangle_ {0}}{(\omega_ {1}+\omega_ {2}+\omega_ {3}+\omega_ {1+2+3})(\omega_ {4}+\omega_ {5}+\omega_ {4+5})}.\]$\left\lvert \Omega \right\rangle_ {3}^{(5)}:$
we have
\[\begin{align*} H_ {3}^{(1)}\left\lvert \Omega \right\rangle_ {2}^{(4)} =& \frac{3 g^3 m}{4 \sqrt{2}} \int \frac{d^{3}p_ {1,2,3,4}}{(2\pi)^{12}} \, \frac{\left\lvert \vec{p}_ {1,2,3,4,-1-2-3-4} \right\rangle_ {0}}{\omega_ {1+2}+\omega_ {3}+\omega_ {4}+\omega_ {1+2+3+4}} \\ &\times \left(2- \frac{9m^{2}}{\omega_ {3+4}(\omega_ {1+2}+\omega_ {3+4}+\omega_ {1+2+3+4})}-\frac{9m^{2}}{\omega_ {1+2+3}(\omega_ {1+2+3}+\omega_ {4}+\omega_ {1+2+3+4})}\right), \\ H_ {3}^{(-1)}\left\lvert \Omega \right\rangle_ {2}^{(6)}=& -\frac{9g^{3}m^{3}}{4\sqrt{2}}\int \frac{d^{3}p_ {1,2,3,4}}{(2\pi)^{12}} \, \left( \frac{\left\lvert \vec{p}_ {1,2,3,-1,-2-3} \right\rangle_ {0}}{\omega_ {4}\omega_ {1+4}(\omega_ {2}+\omega_ {3}+\omega_ {2+3})(\omega_ {1}+\omega_ {4}+\omega_ {1+4})} \right. \\ &\left. + \frac{3\left\lvert \vec{p}_ {2,4,-1-2,1+3,-3-4} \right\rangle_ {0}}{\omega_ {1}\omega_ {3}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})(\omega_ {1}+\omega_ {2}+\omega_ {1+2}+\omega_ {3}+\omega_ {4}+\omega_ {3+4})}\right) , \\ H_ {4}^{(2)}\left\lvert \Omega \right\rangle_ {1}^{(3)} =& -\delta m^{2}\frac{gm}{2\sqrt{2}} \int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}} \, \frac{\left\lvert \vec{p}_ {1,2,3,-1,-2-3} \right\rangle_ {0}}{\omega_ {2}+\omega_ {3}+\omega_ {2+3}} \\ &+ \frac{3g^{3}m}{2\sqrt{2}} \int \frac{d^{3}p_ {1,2,3,4}}{(2\pi)^{12}} \, \frac{\left\lvert \vec{p}_ {1,2,3,-3-4,-1-2+4} \right\rangle_ {0}}{\omega_ {4}(\omega_ {3}+\omega_ {4}+\omega_ {3+4})}. \end{align*}\]Next step would be inversing the $-H_ {2}$, put everything together and simplify, but I’ll leave to later.
$\left\lvert \Omega \right\rangle_ {3}^{(3)}$
We have
\[\begin{align*} H_ {3}^{(-1)}\left\lvert \Omega \right\rangle_ {2}^{(4)} =& \frac{8g^{2}m}{2\sqrt{2}}\int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}} \, \left\lvert \vec{p}_ {1,3,-1-3} \right\rangle_ {0} \left( \frac{1}{2\omega_ {2}\omega_ {1+2}(\omega_ {2}+\omega_ {1+2}+\omega_ {3}+\omega_ {1+3})} \right. \\ &+ \frac{3m^{2}}{\omega_ {2}\omega_ {1+2}\omega_ {1+2+3}(\omega_ {2}+\omega_ {3}+\omega_ {1+2}+\omega_ {1+3})(\omega_ {2}+\omega_ {1+3}+\omega_ {1+2+3})} \\ &\left.+\frac{3m^{2}(2\omega_ {1}+\omega_ {2}+\omega_ {1+2}+\omega_ {3}+\omega_ {1+3})}{4\omega_ {1}\omega_ {2}\omega_ {1+2}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})(\omega_ {1}+\omega_ {3}+\omega_ {1+3})(\omega_ {2}+\omega_ {3}+\omega_ {1+2}+\omega_ {1+3})} \right), \\ H_ {3}^{(-3)}\left\lvert \Omega \right\rangle_ {2}^{(6)} =& \\ H_ {4}^{(0)}\left\lvert \Omega \right\rangle_ {1}^{(3)} =& \frac{gm}{4\sqrt{2}}\int d^{3}x \frac{d^{3}p_ {1,2}}{(2\pi)^{6}}\, \left( \frac{-6\delta m^{2}}{\omega_ {1}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})}+\frac{4A_ {4}'}{(\omega_ {1}+\omega_ {2}+\omega_ {1+2})} \right)\left\lvert \vec{p}_ {1,2,-1-2} \right\rangle_ {0} \\ &+ \frac{9mg^{3}}{4\sqrt{2}}\int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}} \, \frac{\left\lvert \vec{p}_ {1,2,-1-2} \right\rangle_ {0}}{\omega_ {3}\omega_ {1+2+3}(\omega_ {1+2}+\omega_ {3}+\omega_ {1+2+3})} \end{align*}\]$\left\lvert \Omega \right\rangle_ {3}^{(1)}$
We have
\[\begin{align*} H_ {5}^{(1)} \left\lvert \Omega \right\rangle_ {0}^{(0)} =& C_ {1}\left\lvert \vec{p} \right\rangle {\Large\mid}_ {\vec{p}=0} , \\ H_ {3}^{(-3)} \left\lvert \Omega \right\rangle_ {2}^{(4)} =& -\frac{3gm\delta m^{2}}{4\sqrt{2}} \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \frac{\left\lvert \vec{p}=0 \right\rangle_ {0}}{\omega_ {1}^{2}(m+2\omega_ {1})}+\frac{3g^{3}}{4\sqrt{2}}\int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}} \, \frac{\left\lvert \vec{p}=0 \right\rangle_ {0}}{\omega_ {1}\omega_ {1+2}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})} \\ H_ {4}^{(-2)} \left\lvert \Omega \right\rangle_ {1}^{(3)} =& - \delta m^{2} \frac{3gm}{4\sqrt{2}} \int \frac{d^{3}p_ {1}}{(2\pi)} \, \frac{\left\lvert \vec{p}=0 \right\rangle}{\omega_ {1}^{2}(m+2\omega_ {1})}+\frac{3g^{3}}{4\sqrt{2}}\int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}} \, \frac{\left\lvert \vec{p}=0 \right\rangle}{\omega_ {1}\omega_ {1+2}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})}. \end{align*}\]Inverse $-H_ {2}$ and put everything altogether
\[\left\lvert \Omega \right\rangle_ {3}^{(1)} = - \frac{C_ {1}\left\lvert \vec{p}=0 \right\rangle_ {0}}{m}-\frac{3gm\delta m^{2}}{2\sqrt{2}} \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \frac{\left\lvert \vec{p}=0 \right\rangle_ {0}}{\omega_ {1}^{2}(m+2\omega_ {1})}+\frac{3g^{3}}{2\sqrt{2}}\int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}} \, \frac{\left\lvert \vec{p}=0 \right\rangle_ {0}}{\omega_ {1}\omega_ {1+2}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})}\]Let’s apply the no-tadpole condition. Expand and match the coupling, we find the equation involving $H_ {5}$ is
\[_ {3}\left\langle \Omega \right\rvert \phi(\vec{x})\left\lvert \Omega \right\rangle_ {0} = - _ {2}\left\langle \Omega \right\rvert \phi(\vec{x})\left\lvert \Omega \right\rangle_ {1},\]This should allow us to fix a constant parameter ($C_ {1}$ specifically) in $H_ {5}$. The right hand side reduces to
\[\begin{align*} \left\langle \Omega_ {2} \right\rvert\phi(\vec{x})\left\lvert \Omega_ {1} \right\rangle =& \frac{e^{ -i\vec{k}\cdot \vec{x} }}{2m} C_ {1} \\ =&\left\langle \Omega_ {2}^{(4)} \right\rvert\phi(\vec{x})\left\lvert \Omega_ {1}^{(3)} \right\rangle \\ =& -\frac{e^{ -i\vec{k}\cdot \vec{x} }3g^{3}m\left\lvert \Omega_ {0} \right\rangle}{2\sqrt{2}}\int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}} \, \frac{-9m^{2}+\omega_ {1}^{2}+\omega_ {1}(\omega_ {2}+\omega_ {1+2})}{\omega_ {1}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})^{2}(m+\omega_ {1}+\omega_ {2}+\omega_ {1+2})}\\ &+ \frac{-9m^{2}+\omega_ {2}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})}{\omega_ {2}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})^{2}(m+\omega_ {1}+\omega_ {2}+\omega_ {1+2})} \\ &+ \frac{2(-9m^{2}+m\omega_ {1+2}+2\omega_ {1+2}^{2})}{\omega_ {1+2}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})(m+\omega_ {1}+\omega_ {2}+\omega_ {1+2})(m+2\omega_ {1+2})} \end{align*}\]Looks like the integral can not be simplified any more.
Momentum state correction
From $H\left\lvert \vec{p} \right\rangle=\omega _ {p}\left\lvert \vec{p} \right\rangle$, expand it, the $g^{3}$ order part reads
\[(H_ {2}-\omega _ {p} )\left\lvert \vec{p} \right\rangle_ {3} = -H_ {3}\left\lvert \vec{p} \right\rangle_ {2}-H_ {4}\left\lvert \vec{p} \right\rangle_ {1} - H_ {5} \left\lvert \vec{p} \right\rangle_ {0},\]separate into different Fock spaces we get:
\[\begin{align*} (\omega _ {p} -H_ {2})\left\lvert \vec{p} \right\rangle_ {3}^{(10)} =& H_ {3}^{(3)}\left\lvert \vec{p} \right\rangle_ {2}^{(7)} , \\ (\omega _ {p} -H_ {2})\left\lvert \vec{p} \right\rangle_ {3}^{(8)} =& H_ {3}^{(1)}\left\lvert \vec{p} \right\rangle_ {2}^{(7)} + H_ {3}^{(3)}\left\lvert \vec{p} \right\rangle_ {2}^{(5)} + H_ {4}^{(4)}\left\lvert \vec{p} \right\rangle_ {1}^{(4)} , \\ (\omega _ {p} -H_ {2})\left\lvert \vec{p} \right\rangle_ {3}^{(6)} =& H_ {3}^{(-1)}\left\lvert \vec{p} \right\rangle_ {2}^{(7)} + H_ {3}^{(1)}\left\lvert \vec{p} \right\rangle_ {2}^{(5)}+ H_ {3}^{(3)}\left\lvert \vec{p} \right\rangle_ {2}^{(3)} + H_ {4}^{(2)}\left\lvert \vec{p} \right\rangle_ {1}^{(4)}+H_ {4}^{(4)}\left\lvert \vec{p} \right\rangle_ {1}^{(2)} , \\ (\omega _ {p} -H_ {2})\left\lvert \vec{p} \right\rangle_ {3}^{(4)} =& H_ {3}^{(-3)}\left\lvert \vec{p} \right\rangle_ {2}^{(7)} +H_ {3}^{(-1)}\left\lvert \vec{p} \right\rangle_ {2}^{(5)} + H_ {3}^{(1)} \left\lvert \vec{p} \right\rangle_ {2}^{(1)} + H_ {4}^{(0)}\left\lvert \vec{p} \right\rangle_ {1}^{(4)}+ H_ {4}^{(2)}\left\lvert \vec{p} \right\rangle_ {1}^{(2)} +H_ {5}^{(3)}\left\lvert \vec{p} \right\rangle_ {0}^{(1)}, \\ (\omega _ {p} -H_ {2})\left\lvert \vec{p} \right\rangle_ {3}^{(2)} =& H_ {3}^{(-3)}\left\lvert \vec{p} \right\rangle_ {2}^{(5)}+ H_ {3}^{(-1)}\left\lvert \vec{p} \right\rangle_ {2}^{(3)} + H_ {4}^{(0)}\left\lvert \vec{p} \right\rangle_ {1}^{(2)} + H_ {4}^{(-2)}\left\lvert \vec{p} \right\rangle_ {1}^{(4)} +H_ {5}^{(1)}\left\lvert \vec{p} \right\rangle_ {0}^{(1)}, \\ (\omega _ {p} -H_ {2})\left\lvert \vec{p} \right\rangle_ {3}^{(0)} =&H_ {3}^{(-3)} \left\lvert \vec{p} \right\rangle_ {2}^{(3)} +H_ {4}^{(-4)}\left\lvert \vec{p} \right\rangle_ {1}^{(4)}+H_ {4}^{(-2)}\left\lvert \vec{p} \right\rangle_ {1}^{(2)}+H_ {5}^{(-1)}\left\lvert \vec{p} \right\rangle_ {0}^{(1)}=0. \end{align*}\]$\left\lvert \vec{p} \right\rangle_ {3}^{(10)}$
we have
\[H_ {3}^{(3)}\left\lvert \vec{p} \right\rangle_ {2}^{(7)} = - \frac{g^{3}m^{3}}{2\sqrt{2}} \int \frac{d^{3}p_ {1,2,3,4,5,6}}{(2\pi)^{18}} \, \frac{\left\lvert \vec{p},\vec{p}_ {1,2,3,4,5,6,-1-2,-3-4,-5-6} \right\rangle_ {0}}{\omega_ {3}+\omega_ {4}+\omega_ {5}+\omega_ {5}+\omega_ {3+4}+\omega_ {5+6}}\]inverse $\omega _ {p}-H_ {2}$ we get
\[\begin{align*} \left\lvert \vec{p} \right\rangle_ {3}^{10} =&- \frac{g^{3}m^{3}}{2\sqrt{2}} \int \frac{d^{3}p_ {1,2,3,4,5,6}}{(2\pi)^{18}} \, \frac{1}{\omega_ {3}+\omega_ {4}+\omega_ {5}+\omega_ {5}+\omega_ {3+4}+\omega_ {5+6}} \\ &\times \frac{\left\lvert \vec{p},\vec{p}_ {1,2,3,4,5,6,-1-2,-3-4,-5-6} \right\rangle_ {0}}{\omega _ {p} +\omega_ {1}+\omega_ {2}+\omega_ {3}+\omega_ {4}+\omega_ {5}+\omega_ {6}+\omega_ {1+2}+\omega_ {3+4}+\omega_ {5+6}}. \end{align*}\]$\left\lvert \vec{p} \right\rangle_ {3}^{(8)}$
we get
\[\begin{align*} H_ {3}^{(1)}\left\lvert \vec{p} \right\rangle_ {2}^{(7)} =& \\ H_ {3}^{(3)}\left\lvert \vec{p} \right\rangle_ {2}^{(5)} =& \\ H_ {4}^{(4)}\left\lvert \vec{p} \right\rangle_ {1}^{(4)} =& \end{align*}\]$\left\lvert \vec{p} \right\rangle_ {3}^{(6)}$
$\left\lvert \vec{p} \right\rangle_ {3}^{(4)}$
We have
\[H_ {5}\left\lvert \vec{p} \right\rangle_ {0} = C_ {5,3}\int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}} \, \left\lvert \vec{p},\vec{p}_ {1,2,-1-2} \right\rangle + \frac{3C_ {5,3}}{2\omega _ {p} }\int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \left\lvert \vec{p}-\vec{p}_ {f_ {1}},\vec{p}_ {1} \right\rangle + C_ {5,1} \left\lvert \vec{p},0 \right\rangle .\]$\left\lvert \vec{p} \right\rangle_ {3}^{(2)}$
In summary, we have
\[\begin{align*} H_ {3}^{(-3)}\left\lvert \vec{p} \right\rangle_ {2}^{(5)} =& ,\\ H_ {3}^{(-1)}\left\lvert \vec{p} \right\rangle_ {2}^{(3)} =& ,\\ H_ {4}^{(0)}\left\lvert \vec{p} \right\rangle_ {1}^{(2)} =& \frac{3gm A_ {4}'}{2\sqrt{2}\omega _ {p} }\int d^{3}x \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \frac{\left\lvert \vec{p}_ {1},\vec{p}-\vec{p}_ {1} \right\rangle}{-\omega _ {p} +\omega_ {1}+\omega_ {p-p_ {1}}} \\ & - \frac{3gm\delta m^{2}}{2\sqrt{2}\omega _ {p} } \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \frac{\left\lvert \vec{p}_ {1},\vec{p}-\vec{p}_ {1} \right\rangle}{\omega_ {1}(-\omega _ {p} +\omega_ {1}+\omega_ {p-p_ {1}})} \\ &+ \frac{9mg^{3}}{8\sqrt{2}\omega _ {p} } \int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}} \, \frac{\left\lvert \vec{p}_ {1},\vec{p}-\vec{p}_ {1} \right\rangle}{\omega_ {2}\omega_ {p+p_ {2}}(-\omega _ {p} +\omega_ {2}+\omega_ {p+p_ {2}})} \\ H_ {4}^{(-2)}\left\lvert \vec{p} \right\rangle_ {1}^{(4)}=& ,\\ H_ {5}^{(1)}\left\lvert \vec{p} \right\rangle_ {0}^{(1)}=& C_ {5,1} \left\lvert \vec{p},\vec{q}=0 \right\rangle + \frac{3C_ {5,3}}{2\omega _ {p} }\int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \left\lvert \vec{p}_ {1},\vec{p}-\vec{p}_ {1} \right\rangle_ {0} , \end{align*}\]$\left\lvert \vec{p} \right\rangle_ {3}^{(0)}$
Summary of results
I use the shorthand notation $\left\lvert \vec{p}_ {-1-2} \right\rangle:=\left\lvert -\vec{p}_ {1}-\vec{p}_ {2} \right\rangle$, $\left\lvert \vec{p}_ {-1’-2’} \right\rangle:=\left\lvert -\vec{p}’_ {1}-\vec{p}’_ {2} \right\rangle$, $\omega_ {1}=\omega_ {p_ {1}}, \omega_ {1’}=\omega_ {\vec{p}_ {1}’},\omega_ {1+2}=\omega_ {p_ {1}+p_ {2}}$. Multiple indices usually denote tensor product, for example $\left\lvert \vec{p}_ {1,2} \right\rangle:=\left\lvert \vec{p}_ {1} \right\rangle\left\lvert \vec{p}_ {2} \right\rangle=\left\lvert \vec{p}_ {1}\vec{p}_ {2} \right\rangle$, and
\[\frac{d^{3}p_ {1,2,1',2'}}{(2\pi)^{12}} := \frac{d^{3}p_ {1}}{(2\pi)^{3}}\frac{d^{3}p_ {2}}{(2\pi)^{3}}\frac{d^{3}p'_ {1}}{(2\pi)^{3}}\frac{d^{3}p'_ {2}}{(2\pi)^{3}}.\]We also simplify $A_ {p_ {1}}^{\ddagger}$ as $A_ {1}^{\ddagger}$ and $A_ {-p_ {1}-p_ {2}}$ as $A_ {-1-2}$.
Hamiltonians:
In the below is the summary of Hamiltonians updated by Hamiltonian Renormalization Conditions (HRC):
\[\begin{align*} \mathcal{H}_ {0} =& \mathcal{H}_ {1}=0, \\ \mathcal{H}_ {2} =& \frac{\pi^{2}}{2} + \frac{(\partial \phi)^{2}}{2} + \frac{1}{2}m^{2}\phi^{2} \\ H_ {2} =& \int \frac{d^{3}p}{(2\pi)^{3}} \, \omega_ {p} A^{\ddagger}_ {p} A_ {p} , \\ \mathcal{H}_ {3} =& -\frac{mg}{\sqrt{2}} \phi^{3}, \\ H_ {3} =& H_ {3}^{(3)}+H_ {3}^{(1)}+H_ {3}^{(-1)} + H_ {3}^{(-3)} \end{align*}\]where
\[\begin{align*} H_ {3}^{(3)} =& -\frac{mg}{\sqrt{2}} \int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}}\, A_ {1}^{\ddagger}A_ {2}^{\ddagger}A_ {-1-2}^{\ddagger} \\ H_ {3}^{(1)} =& -\frac{mg}{\sqrt{2}} \int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}}\, \frac{3}{2\omega_ {1+2}}A_ {1}^{\ddagger}A_ {2}^{\ddagger}A_ {1+2} \\ H_ {3}^{(-1)} =& -\frac{mg}{\sqrt{2}}\int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}}\,\frac{3}{2\omega_ {2}} \frac{1}{2\omega_ {1+2}} A_ {1}^{\ddagger}A_ {-2} A_ {1+2} \\ H_ {3}^{(-3)} =& -\frac{mg}{\sqrt{2}}\int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}}\, \frac{1}{2\omega_ {1}2\omega_ {2}2\omega_ {1+2}} A_ {-1}A_ {-2}A_ {1+2} . \end{align*}\]In each term the momentum conservation is suggested by the fact that, if we treat the subscript of creation operators as plus momenta, that of the annihilation operators as negative momenta, then their summation gives zero, for example in $A_ {1}^{\ddagger}A_ {2}^{\ddagger}A_ {1+2}$ the total momentum would be (1+2-1-2) which is zero.
and
\[\begin{align*} H_ {4} =& \sum_ {n=0}^{4} H_ {4}^{(4-2n)}, \\ H_ {4}^{(4)} =& \frac{g^{2}}{4} \int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}} \, A^{\ddagger}_ {1}A^{\ddagger}_ {2}A^{\ddagger}_ {3}A^{\ddagger}_ {-1-2-3} ,\\ H_ {4}^{(2)} =& g^{2} \int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}} \, A^{\ddagger}_ {1}A^{\ddagger}_ {2}A^{\ddagger}_ {3} \frac{A_ {1+2+3}}{2\omega_ {1+2+3}} \\ &- \frac{\delta m_ {1}^{2}}{2} \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, A_ {1}^{\ddagger}A_ {-1}^{\ddagger},\\ H_ {4}^{(0)} =& \frac{3g^{2}}{2} \int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}}\, A^{\ddagger}_ {1} A^{\ddagger}_ {2} \frac{A_ {-3}}{2\omega_ {3}}\frac{A_ {1+2+3}}{2\omega_ {1+2+3}} \\ &- \delta m_ {1}^{2} \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \frac{A_ {1}^{\ddagger}A_ {1}}{2\omega_ {1}}+\int d^{3}x \, A_ {4}' ,\\ H_ {4}^{(-2)} =& g^{2}\int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}}\, A^{\ddagger}_ {1} \frac{A_ {-2}}{2\omega_ {2}}\frac{A_ {-3}}{2\omega_ {3}}\frac{A_ {1+2+3}}{2\omega_ {1+2+3}} \\ & -\frac{\delta m_ {1}^{2}}{2}\int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \frac{A_ {1}A_ {-1}}{(2\omega_ {1})^{2}} , \\ H_ {4}^{(-4)} =& \frac{g^{2}}{4} \int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}}\, \frac{A_ {-1}}{2\omega_ {1}}\frac{A_ {-2}}{2\omega_ {2}}\frac{A_ {-3}}{2\omega_ {3}}\frac{A_ {1+2+3}}{2\omega_ {1+2+3}} . \end{align*}\]and
\[\begin{align*} H_ {5}=& H_ {5}^{(3)}+H_ {5}^{(1)}+H_ {5}^{(-1)}+H_ {5}^{(-3)} ,\\ H_ {5}^{(3)}=& C_ {5,3}\int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}}\, A_ {1}^{\ddagger}A_ {2}^{\ddagger}A_ {-1-2}^{\ddagger} ,\\ H_ {5}^{(1)}=& C_ {5,3}\int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}}\, \frac{3}{2\omega_ {1+2}}A_ {1}^{\ddagger}A_ {2}^{\ddagger}A_ {1+2} +C_ {5,1}A_ {0}^{\ddagger} ,\\ H_ {5}^{(-1)}=&C_ {5,3} \int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}}\,\frac{3}{2\omega_ {2}} \frac{1}{2\omega_ {1+2}} A_ {1}^{\ddagger}A_ {-2} A_ {1+2} + C_ {5,1} \frac{A_ {0}}{2m} ,\\ H_ {5}^{(-3)}=& C_ {5,3}\int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}}\, \frac{1}{2\omega_ {1}2\omega_ {2}2\omega_ {1+2}} A_ {-1}A_ {-2}A_ {1+2} ,\\ \end{align*}\]where $C_ {5,i}$ are some combinations of counter terms whose value will be fixed later.
Vacuum states corrections
The corrections to vacuum states:
\[\begin{align*} \left\lvert \Omega \right\rangle_ {1}^{(3)} =& \frac{mg}{\sqrt{2}} \int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}} \, \frac{\left\lvert \vec{p}_ {1,2,-1-2}\right\rangle_ {0} }{(\omega_ {1}+\omega_ {2}+\omega_ {3})}, \\ \left\lvert \Omega \right\rangle_ {2}^{(6)} =&\frac{m^{2}g^{2}}{2} \int \frac{d^{3}p_ {1,2,1',2'}}{(2\pi)^{12}} \\ &\times \frac{\left\lvert \vec{p}_ {1,2,-1-2}\;\vec{p}'_ {1,2,-1-2} \right\rangle_ {0}}{(\omega_ {1}+\omega_ {2}+\omega_ {1+2})(\omega_ {1}+\omega_ {2}+\omega_ {1+2}+\omega_ {1'}+\omega_ {2'}+\omega_ {1'+2'})} \\ \left\lvert \Omega \right\rangle_ {2}^{(4)} =& \frac{g^{2}}{4} \int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}} \, \left( \frac{9m^{2}}{\omega_ {1+2}(\omega_ {1+2}+\omega_ {3}+\omega_ {1+2+3})} -1\right) \\ &\times \frac{\left\lvert \vec{p}_ {1,2,3,-1-2-3} \right\rangle_ {0}}{\omega_ {1}+\omega_ {2}+\omega_ {3}+\omega_ {1+2+3}} ,\\ \left\lvert \Omega \right\rangle_ {3}^{(9)} =& \frac{g^{3}m^{3}}{2\sqrt{2}}\int \frac{d^{3}p_ {1,2,3,4,5,6}}{(2\pi)^{18}} \, \frac{1}{(\omega_ {1}+\omega_ {2}+\omega_ {1+2})(\omega_ {1}+\omega_ {2}+\omega_ {3}+\omega_ {4}+\omega_ {1+2}+\omega_ {3+4})} \\ &\times \frac{\left\lvert \vec{p}_ {1,2,3,4,5,6},-\vec{p}_ {1}-\vec{p}_ {2},-\vec{p}_ {3}-\vec{p}_ {4},-\vec{p}_ {5}-\vec{p}_ {6} \right\rangle}{(\omega_ {1}+\omega_ {2}+\omega_ {3}+\omega_ {4}+\omega_ {5}+\omega_ {6}+\omega_ {1+2}+\omega_ {3+4}+\omega_ {5+6})}\\ \left\lvert \Omega \right\rangle_ {3}^{(7)} =& \frac{g^{3}m}{4\sqrt{2}}\int \frac{d^{3}p_ {1,2,3,4,5}}{(2\pi)^{15}} \, \frac{\left( \frac{9m^{2}}{\omega_ {1+2}(\omega_ {1+2}+\omega_ {3}+\omega_ {1+2+3})}-1 \right)\left\lvert \vec{p}_ {1,2,3,4,5,-1-2-3,-4-5} \right\rangle}{(\omega_ {1}+\omega_ {2}+\omega_ {3}+\omega_ {1+2+3})(\omega_ {4}+\omega_ {5}+\omega_ {4+5})},\\ \left\lvert \Omega \right\rangle_ {3}^{(5)} =& \\ \left\lvert \Omega \right\rangle_ {3}^{(3)} =& \\ \left\lvert \Omega \right\rangle_ {3}^{(1)} =& - \frac{C_ {1}\left\lvert \vec{p}=0 \right\rangle}{m}-\frac{3gm\delta m^{2}}{2\sqrt{2}} \int \frac{d^{3}p_ {1}}{(2\pi)^{3}} \, \frac{\left\lvert \vec{p}=0 \right\rangle}{\omega_ {1}^{2}(m+2\omega_ {1})}+\frac{3g^{3}}{2\sqrt{2}}\int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}} \, \frac{\left\lvert \vec{p}=0 \right\rangle}{\omega_ {1}\omega_ {1+2}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})} \end{align*}\]The momentum eigenstates:
\[\begin{align*} \left\lvert \vec{p} \right\rangle_ {1}^{(2)} =& \frac{3mg}{2\sqrt{2}\omega _ {p} }\int \frac{d^{3}p_ {1}}{(2\pi)^{3}}\, \frac{\left\lvert \vec{p}_ {1},\vec{p} -\vec{p}_ {1} \right\rangle^{(2)}_ {0}}{\omega_ {p_ {1}}+\omega_ {p-p_ {1}}-\omega_ {p}} , \\ \left\lvert \vec{p} \right\rangle_ {1}^{(4)} =& \frac{mg}{\sqrt{2}} \int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}} \, \frac{\left\lvert \vec{p} \, \vec{p}_ {1,2,-1-2} \right\rangle_ {0}^{(4)}}{\omega_ {1}+\omega_ {2}+\omega_ {1+2}}, \\ \left\lvert \vec{p} \right\rangle_ {2}^{(7)} =& \frac{m^{2}g^{2}}{2} \int \frac{d^{3}p_ {1,2,3,4}}{(2\pi)^{12}} \, \frac{\left\lvert \vec{p},\vec{p}_ {1,2,3,4,-1-2,-3-4} \right\rangle_ {0}}{\omega_ {1}+\omega_ {2}+\omega_ {3}+\omega_ {4}+\omega_ {1+2}+\omega_ {3+4}}, \\ \left\lvert \vec{p}\right\rangle_ {2}^{(5)} =& \frac{g^{2}}{4}\int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}} \, \left( \frac{9m^{2}}{\omega_ {2+3}(\omega_ {1}+\omega_ {2+3}+\omega_ {1+2+3})}-1 \right) \frac{\left\lvert \vec{p},\vec{p}_ {1,2,3,-1-2-3} \right\rangle_ {0}}{\omega_ {1}+\omega_ {2}+\omega_ {3}+\omega_ {1+2+3}} \\ &+ \frac{3g^{2}m^{2}}{4\omega _ {p} }\int \frac{d^{3}p_ {1,2,3}}{(2\pi)^{9}} \, \frac{\left\lvert \vec{p}_ {1,2,3,-1-2},\vec{p}-\vec{p}_ {3} \right\rangle_ {0}}{(\omega_ {1}+\omega_ {2}+\omega_ {1+2})(\omega_ {3}+\omega_ {p+p_ {3}}-\omega_ {p})}.\\ \left\lvert \vec{p} \right\rangle_ {2}^{(3)} =& \frac{g^{2}}{4\omega _ {p} }\int \frac{d^{3}p_ {1,2}}{(2\pi)^{6}} \, \left( -2+\frac{9m^{2}}{\omega_ {1+2}}\left( \frac{1}{-\omega _ {p} +\omega_ {p-p_ {1}-p_ {2}}+\omega_ {1+2}} + \frac{1}{\omega_ {1}+\omega_ {2}+\omega_ {1+2}} \right) \right)\\ &\times \frac{\left\lvert \vec{p}_ {1,2},\vec{p}-\vec{p}_ {1}-\vec{p}_ {2} \right\rangle_ {0}}{-\omega _ {p} +\omega_ {1}+\omega_ {2}+\omega_ {p-p_ {1}-p_ {2}}} \end{align*}\]The counter terms:
\[\begin{align*} \delta v_ {1}= &- \frac{m}{\sqrt{2}g} \left( \frac{\delta g}{g}- \frac{\delta m_ {1}^{2}}{2m^{2}}- \frac{\delta m_ {1}^{4}}{2g^{2}} \right) \\ \delta v_ {2} =& 0, \\ A_ {4}' \equiv& \frac{3g^{2}m^{2}}{8} \int d^{3}x\,\frac{d^{3}p_ {1}d^{3}p_ {2}}{(2\pi)^{6}} \, \frac{1}{\omega_ {p_ {1}}\omega_ {p_ {2}}\omega_ {p_ {1}+p_ {2}}(\omega_ {p_ {1}}+\omega_ {p_ {2}}+\omega_ {p_ {1}+p_ {2}})} ,\\ \delta m^{2} =& - \frac{9m^{2}g^{2}}{2}\int \frac{d^{3}p_ {2}}{(2\pi)^{3}} \, \frac{1}{\omega_ {2}\omega_ {1+2}(\omega_ {1}+\omega_ {2}+\omega_ {1+2})} \\ =& - \frac{9g^{2}m^{2}}{8\pi^{2}}\ln\left( \frac{\Lambda}{m} \right) + \text{finite}, \\ \frac{\delta g}{g} =& - \frac{9g^{2}\ln \Lambda}{16\pi^{2}}+\text{finite}. \end{align*}\]where $A_ {4}’$ is the constant part of $H_ {4}$.
Enjoy Reading This Article?
Here are some more articles you might like to read next: