Diagrammatic Rules for Jarah Diagrams
These rules are currently being used by myself and no one else, it is by no means standard or widely accepted. I find it extremely fun to play with those rules and diagrams.
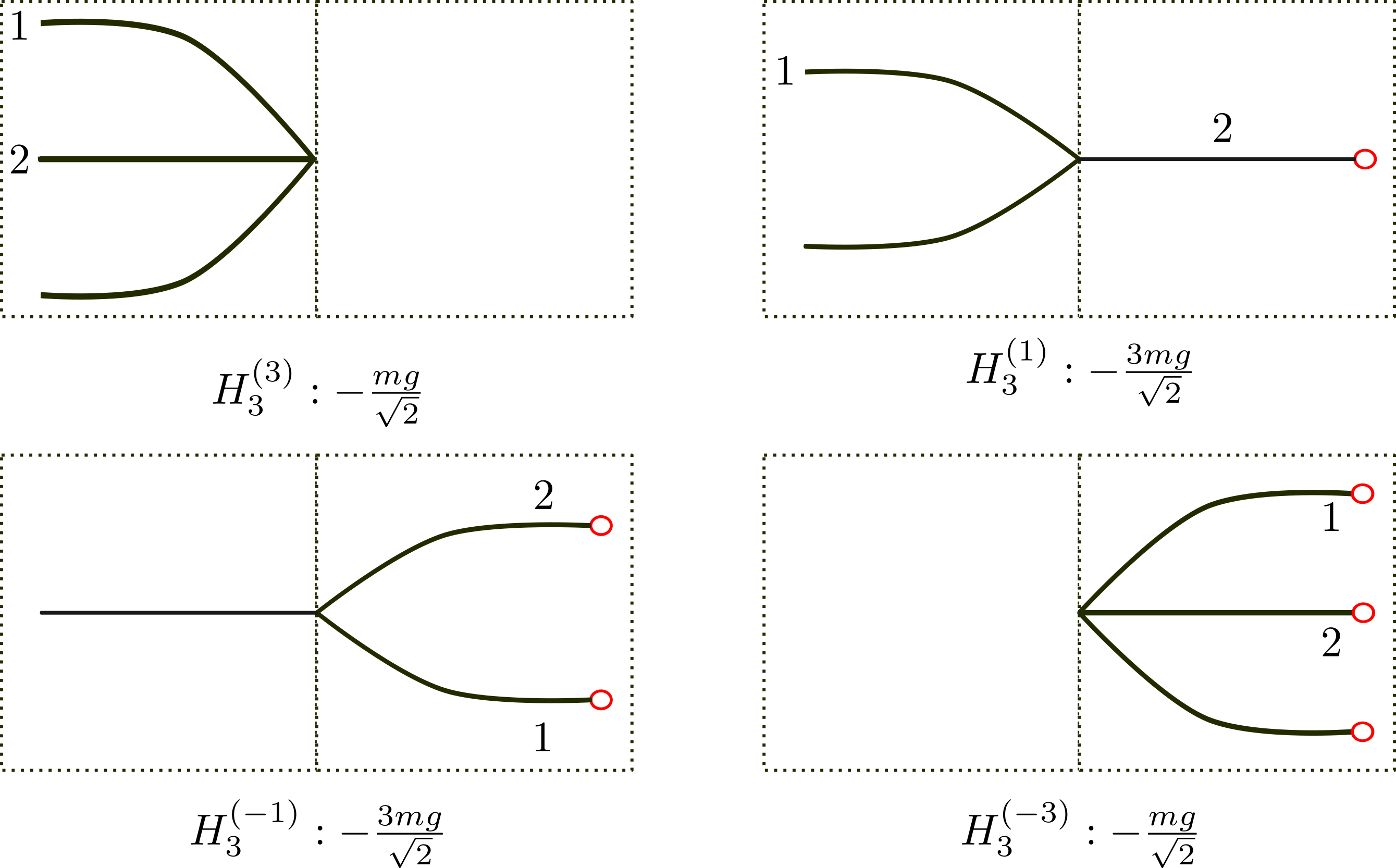
The numbers denote momenta, for example, (1) represents ($\vec{p}_ {1}$). We only label the independent momenta since momentum conservation at each vertex allows us to determine any unlabeled momentum without ambiguity. One source of divergence, specifically, a factor of $(2\pi)^{3}\delta^{3}(0)$ (or equivalently $\int d^{3}x$) arises because the Dirac delta functions over-constrain the momenta. This divergence is also accounted for in the diagrammatic method.
In the following rules, some factors (such as a factor of 3) is perhaps better treated as symmetry factors, but for practical purpose I treat them as part of the definition of the the vertices.
I note that the diagrams I have are used to calculate quantities such as $H_ {3}\left\lvert \vec{p} \right\rangle_ {1},H_ {4}\left\lvert \Omega \right\rangle_ {2}$ only, in order to obtain the final state we need to further invert some operators. The inversion is quite straightforward though.
Rules for Hamiltonians
Rules for $H_ {3}^{(-)}$
Rules for $H_ {4}^{(-)}$
Vertices (a) and (b) contribute a factor of $g^{2}/4$, while vertices (c) and (d) contribute $g^{2}$. Vertex (e), being the most symmetric, gives a factor of $-3g^{2}/2$. Vertices (f), (g), and (h) correspond to the counterterms, contributing factors of $-\delta m^{2}/2$, $-\delta m^{2}$ and $-\delta m^{2}/2$ respectively. Vertex (i) represents the infrared divergence, which is proportional to the total spacetime volume and given by $A’_ {4}(2\pi)^{3}\delta^{3}(0)$.
Feynman-like Rules
With above ingredients we may introduce the rules to connect them now.
Consider the higher order correction to the wave function give by $H_ {\bullet}\left\lvert \psi \right\rangle$, where $H_ {\bullet}$ is any Hamiltonian of order and $\left\lvert \psi \right\rangle$ some initial states whose expression is already know. The diagrams for $H_ {\bullet}$ comprises of a set of vertices, while the diagram for $\left\lvert \psi \right\rangle$ is assumedly known. We need to enumerate all possible ways to attach all vertices to the state diagram. Each red circle from the vertices needs to be connected to another let to form a propagator, otherwise the diagram vanishes. After the connections are made, momenta conservation must hold at each vertex and circle. The procedure is as follows. 1) Identify the diagrams, label all independent momenta. 2) Set up the configuration. Place the vertex diagrams on the left and state on the right, enumerate all possible ways of connecting the circles to the legs from state, forming new diagrams. If multiple equivalent connections exist for the same diagram, their number defines the symmetry factor. 3) Label manipulation. A circle connecting two independently momenta (simply two labels in our notation) is fully labeled; one connects to only a single label is half-labeled. Arrange the labels so that as many circles as possible are fully labeled. Each fully labeled circle conserves the momenta, thus a pair of connected label and circle cancel each other. Remove the circle together with one of the connected momentum labels, then replace the removed circle with an arrow indicating the direction of increasing coupling, yielding a regular propagator. Any circle that can not be removed corresponding to a singular propagator, contributing a factor of $\int d^{3}x$ or equivalently $(2\pi)^{3}\delta^{3}(0)$. 4) Construct the expression. Apply momentum conservation at each vertex to fix the momenta of propagators and external legs. Read the diagram from left to right, include the symmetry factor. The final state can be read off from the leftmost external legs, each corresponds to a momentum eigenvalue. For every independent momentum, write down the integral with measure $\int d^{3}p_ {i} / (2\pi)^{3}$, where $i$ is the corresponding momentum label; for every vertex and propagator, write down the corresponding factors. Finally write down the initial state, this will complete the process and gives us the complete expression.
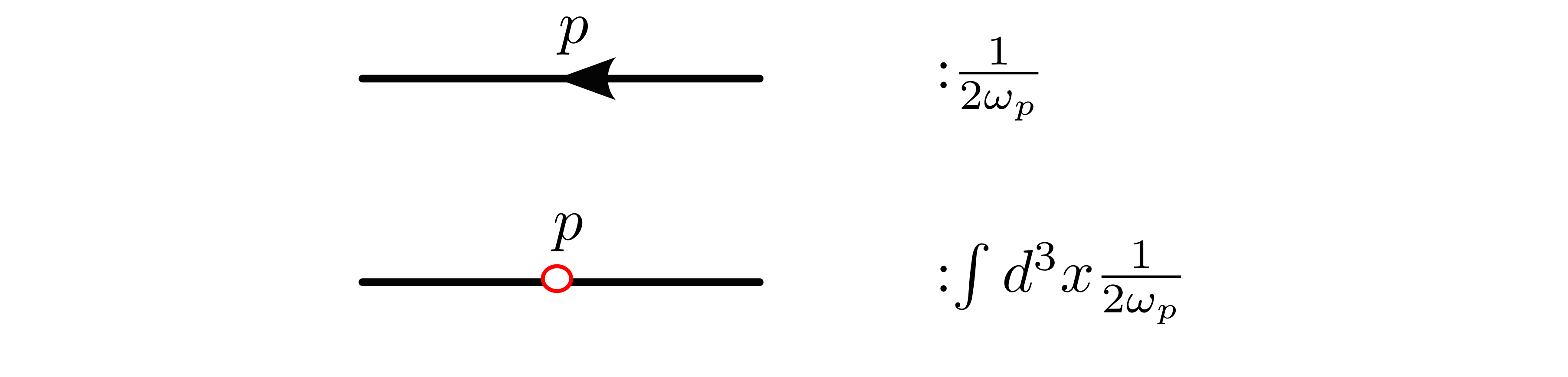
Some examples

Enjoy Reading This Article?
Here are some more articles you might like to read next: